
2020年11月刷题日志

11.30
美好的一周从周一刷题开始结束
题目
767. 重构字符串
难度中等
给定一个字符串
S,检查是否能重新排布其中的字母,使得两相邻的字符不同。若可行,输出任意可行的结果。若不可行,返回空字符串。
示例 1:
输入: S = "aab" 输出: "aba"示例 2:
输入: S = "aaab" 输出: ""注意:
S只包含小写字母并且长度在[1, 500]区间内。
思路
参考了大佬的c++题解
说白了就是贪心
- 用字典统计字母出现次数
- 这里如果某个字母出现的次数超过了字符串长度的一半
- 那肯定是无法重构的,因为最后必然会剩下两个同字符相邻
- 再根据字母的出现次数升序排列
- 构建一个数组,初始化每个位置为0
- 从index = 1的位置开始逐个插入字母,从出现次数最少的开始
- index逐次递增2,插入字母,index出界了就从0开始重新插,插到最后就是答案
代码
class Solution:
def reorganizeString(self, S: str) -> str:
dic = dict()
for i in S:
if i in dic:
dic[i] += 1
else:
dic[i] = 1
if dic[i] > (len(S)+1)//2:
return ""
inds = list(set(S))
inds.sort(key = lambda x:dic[x])
res = [0 for i in range(len(S))]
index = 1
for i in inds:
cnt = dic[i]
char = i
for j in range(cnt):
if index>=len(S):
index = 0
res[index] = char
index += 2
return "".join(res)
11.29
美好的周日从实验室开会和简单题开始
题目
976. 三角形的最大周长
难度简单
给定由一些正数(代表长度)组成的数组
A,返回由其中三个长度组成的、面积不为零的三角形的最大周长。如果不能形成任何面积不为零的三角形,返回
0。示例 1:
输入:[2,1,2] 输出:5示例 2:
输入:[1,2,1] 输出:0示例 3:
输入:[3,2,3,4] 输出:10示例 4:
输入:[3,6,2,3] 输出:8提示:
3 <= A.length <= 100001 <= A[i] <= 10^6
思路
真·简单题
- 对边进行排序,最大的周长必定是数组中三个连续的边长组成的(贪心)
- 所以从后往前遍历三条边,找到能组成三角形的情况,返回周长即最大周长
代码
class Solution:
def largestPerimeter(self, A: List[int]) -> int:
A.sort()
n = len(A)
for i in range(n-3,-1,-1):
if A[i+2]>=A[i+1]+A[i]:
continue
else:
return A[i]+A[i+1]+A[i+2]
return 0
11.28
这一天,又是体测又是知识竞赛又是互联网+路演ppt,人晕了😵
题目
493. 翻转对
难度困难
给定一个数组
nums,如果i < j且nums[i] > 2*nums[j]我们就将(i, j)称作一个*重要翻转对*。你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1] 输出: 2示例 2:
输入: [2,4,3,5,1] 输出: 3注意:
- 给定数组的长度不会超过
50000。- 输入数组中的所有数字都在32位整数的表示范围内。
思路
别问,问就是抄的大佬题解
- 归并排序
- 边排序边计算反转对的数量
代码
class Solution:
def find_pairs(self, nums, left, right):
# 计算可用对数
# 假设nums[left:mid]和nums[mid+1:right]都是升序排列
res, mid = 0, (left+right)//2
# 利用双指针去计算当前可以有多少个匹配项
j = mid+1
for i in range(left, mid+1):
while j<=right and nums[i]>2*nums[j]:
# 当右边找到的数比左边的数两倍还大的时候
# 说明左边数组i位置和剩下的数字都可以和j自称翻转对
# 那就加上这么多对,继续考虑j之后的数字
res += mid-i+1
j += 1
# 当j对应的数字太大了,说明需要增加i对应的数字的大小
return res
def merge_sort(self, nums, nums_sorted, l, r):
if l>= r:
return 0
mid = (l+r)//2
# 每次递归的值就是左数组中的翻转对+右数组中的翻转对+两个数组中交叉的翻转对
res = self.merge_sort(nums, nums_sorted, l, mid)+self.merge_sort(nums, nums_sorted, mid+1, r)+self.find_pairs(nums, l, r)
# 接下来进行归并排序,把左数组和右数组合并成有序的数组
i, j, k = l, mid+1, l
while i<= mid and j<= r:
if nums[i]<=nums[j]:
nums_sorted[k] = nums[i]
i += 1
else:
nums_sorted[k] = nums[j]
j += 1
k += 1
while i<=mid:
nums_sorted[k] = nums[i]
i += 1
k += 1
while j<= r:
nums_sorted[k] = nums[j]
j += 1
k += 1
for k in range(l, r+1):
nums[k] = nums_sorted[k]
return res
def reversePairs(self, nums: List[int]) -> int:
# 归并排序解决问题
if not nums:
return 0
nums_sorted = [0] * len(nums)
return self.merge_sort(nums, nums_sorted, 0, len(nums)-1)
11.27
题目
454. 四数相加 II
难度中等
给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组
(i, j, k, l),使得A[i] + B[j] + C[k] + D[l] = 0。为了使问题简单化,所有的 A, B, C, D 具有相同的长度 N,且 0 ≤ N ≤ 500 。所有整数的范围在 -228 到 228 - 1 之间,最终结果不会超过 231 - 1 。
例如:
输入: A = [ 1, 2] B = [-2,-1] C = [-1, 2] D = [ 0, 2] 输出: 2 解释: 两个元组如下: 1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0 2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0
思路
蛮可惜的,这个思路应该很容易想,但是我却看了题解标题才想出来
- 存两个哈希表(只存一个也可以),一个放A和B中间元素可能的和,另一个放C和D可能的和
- 然后遍历第一个哈希表的键,去看它的相反数在B中的出现次数
代码
class Solution:
def fourSumCount(self, A: List[int], B: List[int], C: List[int], D: List[int]) -> int:
dic1, dic2 = dict(), dict()
# A和B可能的和存入dic1中,C和D可能的和存入dic2中
n = len(A)
for i in range(n):
for j in range(n):
a, b, c, d = A[i], B[j], C[i], D[j]
if a+b in dic1:
dic1[a+b] += 1
else:
dic1[a+b] = 1
if c+d in dic2:
dic2[c+d] += 1
else:
dic2[c+d] = 1
res = 0
for i in dic1.keys():
if -i in dic2:
res += dic1[i]*dic2[-i]
return res
11.26
题目
164. 最大间距
难度困难
给定一个无序的数组,找出数组在排序之后,相邻元素之间最大的差值。
如果数组元素个数小于 2,则返回 0。
示例 1:
输入: [3,6,9,1] 输出: 3 解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。示例 2:
输入: [10] 输出: 0 解释: 数组元素个数小于 2,因此返回 0。说明:
- 你可以假设数组中所有元素都是非负整数,且数值在 32 位有符号整数范围内。
- 请尝试在线性时间复杂度和空间复杂度的条件下解决此问题。
思路
如果忽略线性时间复杂度的说明,则直接排序完遍历数组求相邻元素的最大差距即可
然而困难题显然不是这么简单的(虽然按题解来写的程序时间复杂度O(N)会比库函数排序慢)
-
利用桶排序
- 创建很多个桶
- 把所有的数字放到合适的桶里
- 计算相邻非空桶之间的最大差值
-
比如
nums = [3,6,9,1]- 每个桶装的数字距离就是 (9-1)/(4-1) = 2
- 意味着我们会有这么多个桶,能装的数字范围为
- [0,2)
- [2,4)
- [4,6)
- [6,8)
- [8,10)
- 然后遍历
nums把数字分别装入桶中 - 最后桶的状态
- [1]
- [3]
- []
- [6]
- [9]
- 最后我们发现3-1=2,6-3=3,9-6=3,所以最大差值是3
-
那为什么这么干就是O(N)了呢?
- 我们在把数字装入桶里的时候,只遍历了一边数组
- 在确定最大差值的时候,只遍历了一遍桶
代码
class Solution:
def maximumGap(self, nums: List[int]) -> int:
# 利用桶排序解题
if len(nums)<2:
return 0
# 首先确定桶的长度,每个桶都是等间距
buckt_len = max(1, (max(nums)-min(nums))//(len(nums)-1))
# 最多可能要把数字放到这么多个桶中
buckt_num = (max(nums)-min(nums))//buckt_len+1
buckets = [[] for i in range(buckt_num)]
# 然后把所有的数字放到桶中
min_num = min(nums)
for num in nums:
buckets[(num-min_num)//buckt_len].append(num)
# 然后计算相邻非空桶之间的最大差值
prev = min_num
res = 0
for bucket in buckets:
if not bucket:
continue
res = max(res, min(bucket)-prev)
prev = max(bucket)
return res
11.25
题目
1370. 上升下降字符串
难度简单
给你一个字符串
s,请你根据下面的算法重新构造字符串:
- 从
s中选出 最小 的字符,将它 接在 结果字符串的后面。- 从
s剩余字符中选出 最小 的字符,且该字符比上一个添加的字符大,将它 接在 结果字符串后面。- 重复步骤 2 ,直到你没法从
s中选择字符。- 从
s中选出 最大 的字符,将它 接在 结果字符串的后面。- 从
s剩余字符中选出 最大 的字符,且该字符比上一个添加的字符小,将它 接在 结果字符串后面。- 重复步骤 5 ,直到你没法从
s中选择字符。- 重复步骤 1 到 6 ,直到
s中所有字符都已经被选过。在任何一步中,如果最小或者最大字符不止一个 ,你可以选择其中任意一个,并将其添加到结果字符串。
请你返回将
s中字符重新排序后的 结果字符串 。示例 1:
输入:s = "aaaabbbbcccc" 输出:"abccbaabccba" 解释:第一轮的步骤 1,2,3 后,结果字符串为 result = "abc" 第一轮的步骤 4,5,6 后,结果字符串为 result = "abccba" 第一轮结束,现在 s = "aabbcc" ,我们再次回到步骤 1 第二轮的步骤 1,2,3 后,结果字符串为 result = "abccbaabc" 第二轮的步骤 4,5,6 后,结果字符串为 result = "abccbaabccba"示例 2:
输入:s = "rat" 输出:"art" 解释:单词 "rat" 在上述算法重排序以后变成 "art"示例 3:
输入:s = "leetcode" 输出:"cdelotee"示例 4:
输入:s = "ggggggg" 输出:"ggggggg"示例 5:
输入:s = "spo" 输出:"ops"提示:
1 <= s.length <= 500s只包含小写英文字母。
思路
就按照题目的要求模拟整个过程即可
利用字典来统计每个字母出现的次数,然后对出现的字母进行排序(python里的sort可以直接实现按字典序排序)
代码
class Solution:
def sortString(self, s: str) -> str:
dic = dict()
for i in set(s):
dic[i] = s.count(i)
keys = sorted(list(set(s)))
res = ""
cnt = len(s)
while cnt>0:
for key in keys:
if dic[key]>0:
res += key
dic[key] -= 1
cnt -= 1
for key in keys[::-1]:
if dic[key]>0:
res += key
dic[key] -= 1
cnt -= 1
return res
11.24
题目
222. 完全二叉树的节点个数
难度中等
给出一个完全二叉树,求出该树的节点个数。
说明:
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例:
输入: 1 / \ 2 3 / \ / 4 5 6 输出: 6
思路
- 我不讲武德,直接忽略完全二叉树,广搜直接求结点数
- 时间复杂度O(N)
- 标准答案思路
- 先求出层数
- 然后根据层数算出结点的上下限
- 根据上下限来进行二分确定结点数
- 二分的时候,利用位运算去判断某个结点存不存在
- 时间复杂度O(log²N)
思路
class Solution:
def countNodes(self, root: TreeNode) -> int:
def exist(root, level, mid):
bits, node = 1 << (level-1), root
while node and bits>0:
if bits&mid:
node = node.right
else:
node = node.left
bits>>=1
return node
level = 0
node = root
while node and node.left:
node, level = node.left, level+1
low, high = 1<<level, (1<<(level+1)) -1
mid = 0
while low<high:
mid = (high-low+1)//2 + low
if exist(root, level, mid):
low = mid
else:
high = mid-1
return min(low, mid)
11.23
题目
452. 用最少数量的箭引爆气球
难度中等
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为
x``start,x``end, 且满足xstart ≤ x ≤ x``end,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。给你一个数组
points,其中points [i] = [xstart,xend],返回引爆所有气球所必须射出的最小弓箭数。示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]] 输出:2 解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]] 输出:4示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]] 输出:2示例 4:
输入:points = [[1,2]] 输出:1示例 5:
输入:points = [[2,3],[2,3]] 输出:1提示:
0 <= points.length <= 104points[i].length == 2-231 <= xstart < xend <= 231 - 1
思路
- 贪心算法,只要保证每次射出的箭追求最大利益的方式即可保证最后花最少的箭
- 怎么保证利益最大呢?
- 假设我们有4个气球是
[0,2], [1,3], [2, 4],[4,5] - 一开始我为了射爆第一个气球,至少需要花一根箭,那这个位置无所谓
[0,2]中间任意一个整数即可 - 所以我们一开始
left = 0, right =2 - 再来看第二个气球,
[1,3],我们发现他的左边界是1,右边界是3,和当前的可射范围[0,2]是有交集的 - 所以我们当前仍只需要一根箭,不过范围缩小到
left = 1, right = 2,左边取大的,右边取小的 - 第三个气球依然可以用同一根箭射爆,
left = 2, right = 2 - 到第四个气球的时候,我们发现无法用这根箭射穿了,所以我们需要多花一根箭,同时当前的范围重置为
left = 4,right = 5 - 因此,射爆这四个气球所需要花的最少箭数为2
- 假设我们有4个气球是
- 可以看到这里我们气球的排序是按照右边界从小到大来排序的,这样子才能保证用的箭尽可能少,而且通过一遍遍历就可以求出箭的个数
- 因为这样排序之后,我们箭的发射位置是从最左往最右考虑的,而且是以连续的方式,所以每根箭会考虑尽可能射穿所有相邻的气球
代码
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
# 按照气球结束坐标的大小排序
points.sort(key = lambda x:x[1])
cnt = 1
length = len(points)
if length<1:
return 0
left, right = points[0]
i = 1
while i<len(points):
cur_left, cur_right = points[i]
if cur_left>right:
cnt += 1
left,right = cur_left, cur_right
else:
left = max(cur_left, left)
i += 1
return cnt
11.22
回家度了一天半的假,继续开工
题目
242. 有效的字母异位词
难度简单
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram" 输出: true示例 2:
输入: s = "rat", t = "car" 输出: false说明: 你可以假设字符串只包含小写字母。
进阶: 如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
思路
就用哈希表(字典)去存取每个字符串中字母出现的次数就行了
这里有一个比较节省空间的技巧是只开辟一个字典
同时遍历两个字符串,将s中字符对应的键值+1,t中字符对应的键值-1
最后遍历字典的key值,如果有不等于0的key就返回false,全为0则返回true
代码
from collections import defaultdict
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
dic_s, dic_t = defaultdict(int), defaultdict(int)
if len(s) != len(t):
return False
for i in range(len(s)):
dic_s[s[i]] += 1
dic_t[t[i]] += 1
return dic_s == dic_t
11.21
题目
148. 排序链表
难度中等
给你链表的头结点
head,请将其按 升序 排列并返回 排序后的链表 。进阶:
你可以在
O(n log n)时间复杂度和常数级空间复杂度下,对链表进行排序吗?示例 1:
输入:head = [4,2,1,3] 输出:[1,2,3,4]示例 2:
输入:head = [-1,5,3,4,0] 输出:[-1,0,3,4,5]示例 3:
输入:head = [] 输出:[]提示:
- 链表中节点的数目在范围
[0, 5 * 104]内-105 <= Node.val <= 105
思路
刷了这么久的题,第一个想法仍然是用内置的sort函数,果然是中了偷🐔的毒
只能看正经的题解
- 递归版归并排序
- 时间复杂度O(NlogN),空间复杂度O(logN)
- 迭代版归并排序
- 时间复杂度O(NlogN),空间复杂度O(1)
- 不思进取,我今天只追求能看懂递归版的
- 首先归并排序的整体思路是
- 把需要排列的链表看成两段
- 前半段和后半段
- 如果前半段是有序的,后半段是有序的,我就可以将两段有序的链表合并成一个有序的链表
- 此处假设前后半段均为有序即递归
- 每次需要做的就是
- 先用快满指针把两个链表切成两端
- 利用递归确定好两个排完序的链表的头节点
- 利用双指针,将两个有序链表合并成一个有序链表
代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def sortList(self, head: ListNode) -> ListNode:
# 首先用快慢指针将链表分成两段
if not head or not head.next:
return head
slow,fast=head,head.next
while fast and fast.next:
slow=slow.next
fast=fast.next.next
# 此时slow指向中间结点或者是前半部分的最后一个结点
tmp = slow.next
slow.next = None
# 将前后段链表进行排序
left, right = self.sortList(head), self.sortList(tmp)
dummy = ListNode(0)
new_head = dummy
# 利用双指针合并两个有序链表
while left and right:
if left.val<right.val:
new_head.next = left
left = left.next
else:
new_head.next = right
right = right.next
new_head = new_head.next
if left:
new_head.next = left
else:
new_head.next = right
return dummy.next
11.20
题目
147. 对链表进行插入排序
难度中等
对链表进行插入排序。
插入排序的动画演示如上。从第一个元素开始,该链表可以被认为已经部分排序(用黑色表示)。 每次迭代时,从输入数据中移除一个元素(用红色表示),并原地将其插入到已排好序的链表中。
插入排序算法:
插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
重复直到所有输入数据插入完为止。
示例 1:
输入: 4->2->1->3 输出: 1->2->3->4示例 2:
输入: -1->5->3->4->0 输出: -1->0->3->4->5
思路
一开始自己写,虽然过了,但是插入排序写了四十多行的代码简直了🤮
看题解优化了一下自己的解法
自己主要是没设置dummyhead导致的代码丑陋
改了之后好看多了
代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def insertionSortList(self, head: ListNode) -> ListNode:
if not head:
return head
dummy = ListNode(0)
dummy.next = head
cur_node = head.next
last_node = head
while cur_node:
if cur_node.val>=last_node.val:
last_node = last_node.next
else:
prev = dummy
while prev.next.val<cur_node.val:
prev = prev.next
last_node.next = cur_node.next
cur_node.next = prev.next
prev.next = cur_node
cur_node = last_node.next
return dummy.next
11.19
完了嘛这不是,简单题都不会做了
题目
283. 移动零
难度简单
给定一个数组
nums,编写一个函数将所有0移动到数组的末尾,同时保持非零元素的相对顺序。示例:
输入: [0,1,0,3,12] 输出: [1,3,12,0,0]说明:
- 必须在原数组上操作,不能拷贝额外的数组。
- 尽量减少操作次数。
思路
又看了题解
-
将非零的数字移到数组前部,然后将后面的位置全部置零即可
-
双指针
- 新建两个指针指向头部
i,j=0,0 i表示当前遍历到的非零的数字的个数j表示当前遍历的所有数字的个数
- 新建两个指针指向头部
-
利用
j去遍历所有的数字,然后把所有非零的数字填充到i的位置 -
每次填充的时候令
i指针后移
代码
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
i, j = 0, 0
while j<len(nums):
if nums[j]!=0:
nums[i] = nums[j]
i += 1
j += 1
for k in range(i, len(nums)):
nums[k] = 0
11.18
题目
134. 加油站
难度中等488
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油
gas[i]升。你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油
cost[i]升。你从其中的一个加油站出发,开始时油箱为空。如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
- 如果题目有解,该答案即为唯一答案。
- 输入数组均为非空数组,且长度相同。
- 输入数组中的元素均为非负数。
示例 1:
输入: gas = [1,2,3,4,5] cost = [3,4,5,1,2] 输出: 3 解释: 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。 因此,3 可为起始索引。示例 2:
输入: gas = [2,3,4] cost = [3,4,3] 输出: -1 解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。 我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油 开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油 开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油 你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。 因此,无论怎样,你都不可能绕环路行驶一周。
思路
- 别的不会,就会死算,直接模拟了一遍从每个加油站出发的情况
- 时间复杂度是O(N²)
- 以为过不了,结果

- 看了题解发现这原来是一道脑筋急转弯的题目
- 或者用数学可以证明
- 假设从加油站
i出发,到j加油站的发现油不够了 - 则无论从
i~j-1之间,任意一个加油站出发,最终到j加油站都会不够油- 因为之前
i出发肯定剩余油量>=0嘛,在i之后出发甚至连之前剩余的油都没了
- 因为之前
- 所以我们可以直接从
j开始重新尝试出发
- 假设从加油站
- 如果最后尝试的起点超过了终点,则说明无法环路行驶
代码
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
diffs = []
for i in range(len(gas)):
diffs.append(gas[i]-cost[i])
# 找到一段累加和一直为0的一段序列
start = 0
while start<len(diffs):
tmp = 0
for i in range(len(diffs)):
index = (start+i)%len(diffs)
tmp += diffs[index]
if tmp<0:
start = start + i + 1
break
else:
return start
return -1
11.17
ohhh 简单题
题目
1030. 距离顺序排列矩阵单元格
难度简单
给出
R行C列的矩阵,其中的单元格的整数坐标为(r, c),满足0 <= r < R且0 <= c < C。另外,我们在该矩阵中给出了一个坐标为
(r0, c0)的单元格。返回矩阵中的所有单元格的坐标,并按到
(r0, c0)的距离从最小到最大的顺序排,其中,两单元格(r1, c1)和(r2, c2)之间的距离是曼哈顿距离,|r1 - r2| + |c1 - c2|。(你可以按任何满足此条件的顺序返回答案。)示例 1:
输入:R = 1, C = 2, r0 = 0, c0 = 0 输出:[[0,0],[0,1]] 解释:从 (r0, c0) 到其他单元格的距离为:[0,1]示例 2:
输入:R = 2, C = 2, r0 = 0, c0 = 1 输出:[[0,1],[0,0],[1,1],[1,0]] 解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2] [[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。示例 3:
输入:R = 2, C = 3, r0 = 1, c0 = 2 输出:[[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]] 解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2,2,3] 其他满足题目要求的答案也会被视为正确,例如 [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]]。提示:
1 <= R <= 1001 <= C <= 1000 <= r0 < R0 <= c0 < C
思路
- 对所有需要考虑的点进行排序即可
代码
class Solution:
def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:
res= []
for i in range(R):
for j in range(C):
res.append([i,j])
res.sort(key = lambda x: (abs(x[0]-r0)+abs(x[1]-c0)))
return res
11.16
another and another vegetable day
题目
406. 根据身高重建队列
难度中等
假设有打乱顺序的一群人站成一个队列。 每个人由一个整数对
(h, k)表示,其中h是这个人的身高,k是排在这个人前面且身高大于或等于h的人数。 编写一个算法来重建这个队列。注意: 总人数少于1100人。
示例
输入: [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] 输出: [[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
思路
又要看题解做题 🤨
- 贪心法
- 从矮到高一个个分配位置
- 这样可以保证先放的人的位置不会对后放的人的位置造成影响
- 因为每个人的整数对(h, k)只记录了在ta前面的身高大于ta的人数
- 因为这道题一定有解,所以按照一定的规则逐个插入就能得到合法解
- 利用python自带的排序方法,按照优先考虑h,再考虑k的方法进行排序
- 把身高低的人拍到前面
- 如果身高相同,就把k大的先放到前面
- 这里也是贪心法的思想,因为需要先插入这些k值大的人
- 例如
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
- 排序完之后就会变成
[[4,4], [5,2], [5,0], [6,1], [7,1], [7,0]]
- 然后初始化一个最后的排序完的数组
resres = [0, 0, 0, 0, 0, 0]- 0说明这个位置还没有人
- 然后按照排序完之后的人员来进行插入
- 此时不需要考虑身高,因为已经是按照从矮到高排序
- 根据k值,从头开始遍历
res数组 - 找到k个0之后的一个空位,就是自己需要插入的位置
[4.4]第一个进行插入操作,一开始数组里都是空位,所以ta找到4个空位后,自然会插入第5个空位res = [0, 0, 0, 0, [4,4], 0]
- 这个时候开始找第二个人的位置,ta是
[5,2],所以从头开始找到两个空位之后,就会插入第三个空位res = [0, 0, [5,2], 0, [4,4], 0]
- 直到把所有人都安排好位置,就可以返回数组
res - 本题贪心法思想理解
- 其实每次插入一个人的时候,队伍里的人的身高都不超过ta
- 又由于我们是根据k值降序,所以和ta同样身高的人,如果k比ta大,那么肯定已经被插到队伍的后面去了,所以不用管
- 如果k比ta小,那么之后自然会插入ta的前面
- 所以ta能够不顾及他人的身高,只看空位数就能找到自己应该待的位置
- 一言以蔽之,把越是不会影响其他人的位置的人越先插到队伍里
代码
class Solution:
def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
# 首先将所有人按身高的从低到高排序
people.sort(key = lambda x: (x[0], -x[1]))
length = len(people)
res = [0 for i in range(length)]
for person in people:
# 找空插入这个人
space = person[1]+1
for i in range(length):
if not res[i]:
space -= 1
if space == 0:
res[i] = person
return res
11.15
another vegetable day
题目
402. 移掉K位数字
难度中等
给定一个以字符串表示的非负整数 num,移除这个数中的 k 位数字,使得剩下的数字最小。
注意:
- num 的长度小于 10002 且 ≥ k。
- num 不会包含任何前导零。
示例 1 :
输入: num = "1432219", k = 3 输出: "1219" 解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。示例 2 :
输入: num = "10200", k = 1 输出: "200" 解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。示例 3 :
输入: num = "10", k = 2 输出: "0" 解释: 从原数字移除所有的数字,剩余为空就是0。
思路
- 从数字的最左侧开始维护一个递增栈,最后返回整个递增栈能构成的数字并去除前导零
- 例如num=‘12342013’, k=2
- 我们要去掉的就是34
- 首先开辟一个栈
- 往栈里开始放数字
- [1]
- [1,2]
- [1,2,3]
- [1,2,3,4]
- 此时我们发现,现在要放的数字是2,但是把2放进这个栈,那这个栈就不是递增的了呀
- 所以,我们就要把栈顶元素pop掉,每pop一个数,代表了我们就用掉了一次移出数字的机会
- 当我们没有移除数字的机会(k==0)或者现在栈顶元素已经比我们当前这个数字小的时候
- 就可以继续往栈里放数字啦
- 直到把整个num字符串遍历完为止
- 如果我们在遍历完之后还有删除数字的机会,那我们就把最后放到栈里的几个数字去掉即可
- 最后把栈拼接成一个字符串并去除前导零
代码
class Solution:
def removeKdigits(self, num: str, k: int) -> str:
nums = []
for i in num:
while nums and i<nums[-1] and k:
nums.pop()
k-=1
nums.append(i)
if k>0:
nums = nums[:-k]
return ''.join(nums).lstrip('0') or "0"
11.14
芜湖,周末简单题
题目
1122. 数组的相对排序
难度简单
给你两个数组,
arr1和arr2,
arr2中的元素各不相同arr2中的每个元素都出现在arr1中对
arr1中的元素进行排序,使arr1中项的相对顺序和arr2中的相对顺序相同。未在arr2中出现过的元素需要按照升序放在arr1的末尾。示例:
输入:arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6] 输出:[2,2,2,1,4,3,3,9,6,7,19]提示:
arr1.length, arr2.length <= 10000 <= arr1[i], arr2[i] <= 1000arr2中的元素arr2[i]各不相同arr2中的每个元素arr2[i]都出现在arr1中
思路
- 没啥好写的,上代码吧
代码
class Solution:
def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
dic = dict()
# 第一遍遍历arr1 统计每个元素的出现次数
for i in arr1:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
res = []
# 第一遍遍历arr2 输出对应元素
for i in arr2:
res += dic[i]*[i]
dic[i] = 0
# 第二遍遍历arr1 输出未在arr2中出现的元素
tmp = []
for i in arr1:
if dic[i]>0:
tmp.append(i)
return res+sorted(tmp)
11.13
题目
328. 奇偶链表
难度中等
给定一个单链表,把所有的奇数节点和偶数节点分别排在一起。请注意,这里的奇数节点和偶数节点指的是节点编号的奇偶性,而不是节点的值的奇偶性。
请尝试使用原地算法完成。你的算法的空间复杂度应为 O(1),时间复杂度应为 O(nodes),nodes 为节点总数。
示例 1:
输入: 1->2->3->4->5->NULL 输出: 1->3->5->2->4->NULL示例 2:
输入: 2->1->3->5->6->4->7->NULL 输出: 2->3->6->7->1->5->4->NULL说明:
- 应当保持奇数节点和偶数节点的相对顺序。
- 链表的第一个节点视为奇数节点,第二个节点视为偶数节点,以此类推。
思路
可恶,要原地算法,偷不了🐔了
- 一个odd结点指向head,一个even结点指向head.next,一个even_head结点指向head.next
- 两个结点向后遍历,例如1->2->3->4
- 把even的下一个结点作为odd的下一个结点
- 1->3
- 把odd指针后移
- odd = 3
- 把odd的后一个结点作为even的下一个结点
- 2->4
- 把even指针后移
- even = 4
- 当前遍历完之后就变成了1->3, 2->4
- 把even的下一个结点作为odd的下一个结点
- 直到遍历到even结点为空或者even没有下一个结点
- 最后把odd的next指针指向even_head即可
代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def oddEvenList(self, head: ListNode) -> ListNode:
if not head:
return head
odd = head
even = head.next
even_head = head.next
while even and even.next:
odd.next = even.next
odd = odd.next
even.next = odd.next
even = even.next
odd.next = even_head
return head
11.12
题目
922. 按奇偶排序数组 II
难度简单
给定一个非负整数数组
A, A 中一半整数是奇数,一半整数是偶数。对数组进行排序,以便当
A[i]为奇数时,i也是奇数;当A[i]为偶数时,i也是偶数。你可以返回任何满足上述条件的数组作为答案。
示例:
输入:[4,2,5,7] 输出:[4,5,2,7] 解释:[4,7,2,5],[2,5,4,7],[2,7,4,5] 也会被接受。提示:
2 <= A.length <= 20000A.length % 2 == 00 <= A[i] <= 1000
思路
既然对空间复杂度没有要求我就直接偷懒了
- 新建数组
tmp1,tmp2 - 遍历数组A,把里面的奇数放到tmp1里,偶数放到tmp2里
- 然后最后循环从tmp1里取一个,tmp2里取一个,生成答案数组
代码
class Solution:
def sortArrayByParityII(self, A: List[int]) -> List[int]:
res = []
tmp1, tmp2 = [], []
for i in A:
if i%2==1:
tmp1.append(i)
else:
tmp2.append(i)
for i in range(len(tmp1)):
res+=[tmp2[i], tmp1[i]]
return res
11.11
没想到剁完手还能敲代码,差点忘了这每日一题
514. 自由之路
难度困难143
电子游戏“辐射4”中,任务“通向自由”要求玩家到达名为“Freedom Trail Ring”的金属表盘,并使用表盘拼写特定关键词才能开门。
给定一个字符串 ring,表示刻在外环上的编码;给定另一个字符串 key,表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。
最初,ring 的第一个字符与12:00方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐,然后按下中心按钮,以此逐个拼写完 key 中的所有字符。
旋转 ring 拼出 key 字符 key[i] 的阶段中:
- 您可以将 ring 顺时针或逆时针旋转一个位置,计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐,并且这个字符必须等于字符 key[i] 。
- 如果字符 key[i] 已经对齐到12:00方向,您需要按下中心按钮进行拼写,这也将算作 1 步。按完之后,您可以开始拼写 key 的下一个字符(下一阶段), 直至完成所有拼写。
示例:
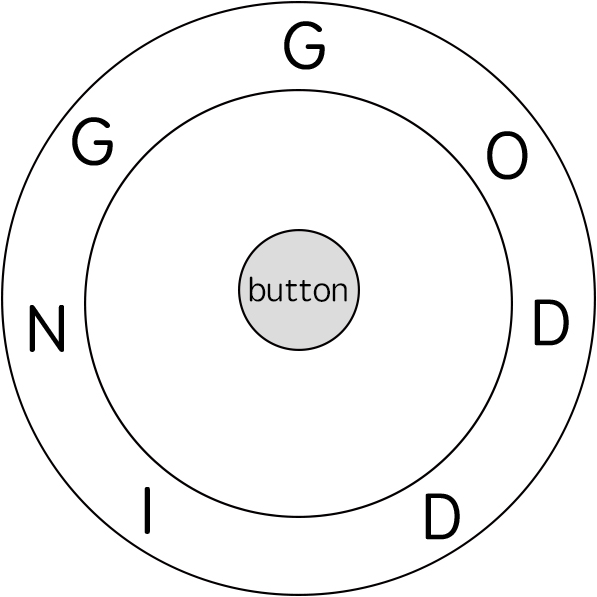
输入: ring = "godding", key = "gd" 输出: 4 解释: 对于 key 的第一个字符 'g',已经在正确的位置, 我们只需要1步来拼写这个字符。 对于 key 的第二个字符 'd',我们需要逆时针旋转 ring "godding" 2步使它变成 "ddinggo"。 当然, 我们还需要1步进行拼写。 因此最终的输出是 4。提示:
- ring 和 key 的字符串长度取值范围均为 1 至 100;
- 两个字符串中都只有小写字符,并且均可能存在重复字符;
- 字符串 key 一定可以由字符串 ring 旋转拼出。
题解
在这里先推荐一个大佬的题解,看完之后半小时以内就能自己敲出来
整体采取动态规划和bfs的思路
- 我们要确保的是最后最优解,中途只要尽量最优即可
- 最重要的是保存多种可能路径,还得保证不去记录肯定不可能是最优解的路径
这次要用的关键数据结构是字典
-
首先我们建立一个空字典
dic- 这个字典用来存放每个字母的位置
-
遍历
ring来初始化dic字典-
dic的所有keys就是ring中出现过的字母 -
每种字母对应key也是一个字典
- 这个字典记录的是:这种字母出现的位置和已经操作的步数(初始化时步数均为0)
-
例如
ring = abcdac -
初始化字典后
dic = {'a':{0:0, 4:0}, 'b':{1:0}, 'c':{2:0,5:0}, 'd':{3:0}}
-
-
然后去遍历
key- 根据每个字母和上一次出现的字母,去更新
dic - 例如
key = cab - 假设我们当前遍历的是
c,那么我们可以看到dic[‘c’]={2:0,5:0} - 我们遍历的上一个位置是0(即起点开始),我们知道走到2至少要2步(向右走),走到5至少要1步(向左走)
- 所以我们更新
dic['c']={2:3, 5:2}(走步数+按1步) - 接下去找下一个字母
a - 我们可以看到
dic['a']={0:0, 4:0},要走到0,至少要1步(从5出发),要走到4也是至少1步(从5出发) - 所以我们更新
dic['a']={0:1+2+1, 4:1+2+1}(本次走的步数+之前走的步数+按1步)
- 根据每个字母和上一次出现的字母,去更新
-
遍历完整个
key之后,字典中对应的key的最后一个字母的字典的values中的最小值,就是答案 -
这边有两个小技巧没提及,代码里实现了,读者可以自己思考
- 如何找到最短步数
- 如何保证一开始是从0出发
代码
class Solution:
def findRotateSteps(self, ring: str, key: str) -> int:
dic = dict()
# 首先初始化字典,把每种字母转换成一个字典
for word in set(list(ring)):
# dic['a'] = {a出现的第一个位置: 0, a出现的第二个位置: 0...}
tmp = dict()
for i in range(len(ring)):
if ring[i] == word:
tmp[i] = 0
dic[word] = tmp
# 然后根据当前的字典去找最短路
last_word = ring[0]
head = True
for word in key:
# 每次更新dic[word]对应的字典
for i in dic[word].keys():
min_dis = float("inf")
target = i
for j in dic[last_word].keys():
start = j
last_dis = dic[last_word][j]
if head:
start = 0
# 正向走到对应字母所需要的距离
foward_dis = abs(start-target)
# 逆向
backword_dis = len(ring)-foward_dis
min_dis = min(min_dis,backword_dis+last_dis, foward_dis+last_dis)
dic[word][i] = min_dis+1
head = False
last_word = word
return min(dic[key[-1]].values())
11.10
题目
31. 下一个排列
难度中等
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须**原地**修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3→1,3,23,2,1→1,2,31,1,5→1,5,1
思路
想了半天,最终还是看了题解
-
整体思想是找到一个小数和一个大数,要保证这个大数在小数后面,然后交换
-
首先从后往前遍历,找到我们需要交换的一个小数
- 例如1,2,3,4,8,7,3
- 可以看到7到3是降序,8到7也是降序
- 但是4到6是升序
- 那么就取4作为我们的小数
-
然后从后往前,找一个大数
- 首先看到3,3比4小,不能作为大数
- 7比4大,所以就选它作为大数
-
交换大数和小数
- 变成1,2,3,7,8,4,3
-
但是我们可以看到,这样子并不是严格的下一个排列
- 因为1,2,3,7,3,4,8才是
-
所以需要给现在大数的所在位置即7的位置之后的序列,重新排序,排列成升序
-
由于我们知道8 4 3是降序排列的,所以从两边开始两两调换元素的位置就能变成升序序列
代码
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
i = len(nums)-2
# 从后往前找需要交换的小数
while i>=0 and nums[i]>nums[i+1]:
i -= 1
# 此时nums[i+1:]都是降序 且num[i]<nums[i+1]
# i位置的数就是我们要找的小数
# 从后往前找 找到尽可能小的大数
if i>=0:
j = len(nums)-1
while j>=0 and nums[i]>=nums[j]:
j -= 1
nums[i], nums[j] = nums[j], nums[i]
# 将小数后面进行升序排列
left = i+1
right = len(nums)-1
while left<right:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right -= 1
11.9
😴
题目
973. 最接近原点的 K 个点
难度中等
我们有一个由平面上的点组成的列表
points。需要从中找出K个距离原点(0, 0)最近的点。(这里,平面上两点之间的距离是欧几里德距离。)
你可以按任何顺序返回答案。除了点坐标的顺序之外,答案确保是唯一的。
示例 1:
输入:points = [[1,3],[-2,2]], K = 1 输出:[[-2,2]] 解释: (1, 3) 和原点之间的距离为 sqrt(10), (-2, 2) 和原点之间的距离为 sqrt(8), 由于 sqrt(8) < sqrt(10),(-2, 2) 离原点更近。 我们只需要距离原点最近的 K = 1 个点,所以答案就是 [[-2,2]]。示例 2:
输入:points = [[3,3],[5,-1],[-2,4]], K = 2 输出:[[3,3],[-2,4]] (答案 [[-2,4],[3,3]] 也会被接受。)提示:
1 <= K <= points.length <= 10000-10000 < points[i][0] < 10000-10000 < points[i][1] < 10000
思路
要偷懒还是很好偷的
直接用个库函数排序然后切片就解决问题了
class Solution:
def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
points.sort(key = lambda x:x[0]**2+x[1]**2)
return points[:K]
但这不就是耍流氓吗 还是用优先队列吧
简单来说就是用优先队列(大根堆)这个数据结构来维护一组点
保证这组点的数量一直小于等于K,且他们是当前遍历到的离原点最近的点
具体怎么做到呢
-
先往堆里放前K个点,按照
(-距离平方,点的index)的格式- 之所以是距离平方是因为,python里优先队列是小根堆,所以为了把距离过长的在维护堆得时候去掉,就要取相反数
-
再继续遍历剩下的点
- 碰到距离比小根堆顶(也就是-距离平方最小的点)要小的
- 就放到小根堆里
- 并移除堆顶元素
- 碰到距离比小根堆顶(也就是-距离平方最小的点)要小的
-
直到遍历结束
代码
class Solution:
def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
res = []
for i in range(K):
x,y = points[i]
res.append((-x**2-y**2,i))
heapq.heapify(res)
for i in range(K,len(points)):
x,y = points[i]
dis = -x**2-y**2
if dis>res[0][0]:
heapq.heappushpop(res, (dis, i))
return [points[i[1]] for i in res]
11.8
题目
122. 买卖股票的最佳时机 II
难度简单938
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4] 输出: 7 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。示例 2:
输入: [1,2,3,4,5] 输出: 4 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。示例 3:
输入: [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。提示:
1 <= prices.length <= 3 * 10 ^ 40 <= prices[i] <= 10 ^ 4
思路
虽然是简单题,但是最后还是看了题解
果然还是没能理解动归的精髓
-
用两个变量来记录
- 某一天不拥有股票时的最大利润 =
d0 - 某一天拥有股票时的最大利润 =
d1
- 某一天不拥有股票时的最大利润 =
-
遍历整个prices数组,并动态更新这两个变量
-
某一天不拥有股票有两种可能
- 当天卖出了股票
- 当天和前一天都未买入
dp0=max(dp0,dp1+prices[i]) -
某一天拥有股票有两种可能
- 当天买入了股票
- 之前买入了股票
dp1=max(dp0-prices[i],dp1) -
遍历完数组后,
dp0就是最后的最大收益值
代码
class Solution:
def maxProfit(self, prices: List[int]) -> int:
# 动态规划
dp0, dp1 = 0, -prices[0]
# 用两个变量来存储某一天手中无股票和手中有股票时的最大利润
for price in prices:
dp0 = max(dp1+price, dp0)
dp1 = max(dp1, dp0-price)
return dp0
11.7
life sucks
11.6
计网人,咬咬牙
题目
1356. 根据数字二进制下 1 的数目排序
难度简单37
给你一个整数数组
arr。请你将数组中的元素按照其二进制表示中数字 1 的数目升序排序。如果存在多个数字二进制中 1 的数目相同,则必须将它们按照数值大小升序排列。
请你返回排序后的数组。
示例 1:
输入:arr = [0,1,2,3,4,5,6,7,8] 输出:[0,1,2,4,8,3,5,6,7] 解释:[0] 是唯一一个有 0 个 1 的数。 [1,2,4,8] 都有 1 个 1 。 [3,5,6] 有 2 个 1 。 [7] 有 3 个 1 。 按照 1 的个数排序得到的结果数组为 [0,1,2,4,8,3,5,6,7]示例 2:
输入:arr = [1024,512,256,128,64,32,16,8,4,2,1] 输出:[1,2,4,8,16,32,64,128,256,512,1024] 解释:数组中所有整数二进制下都只有 1 个 1 ,所以你需要按照数值大小将它们排序。示例 3:
输入:arr = [10000,10000] 输出:[10000,10000]示例 4:
输入:arr = [2,3,5,7,11,13,17,19] 输出:[2,3,5,17,7,11,13,19]示例 5:
输入:arr = [10,100,1000,10000] 输出:[10,100,10000,1000]提示:
1 <= arr.length <= 5000 <= arr[i] <= 10^4
代码
class Solution:
def sortByBits(self, arr: List[int]) -> List[int]:
def countOne(num):
return (bin(num).count('1'), num)
arr.sort(key = countOne)
return arr
11.5
抄作业了抄作业了
不使用优化的解法python直接超时了

题目
127. 单词接龙
难度中等
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典中的单词。
说明:
- 如果不存在这样的转换序列,返回 0。
- 所有单词具有相同的长度。
- 所有单词只由小写字母组成。
- 字典中不存在重复的单词。
- 你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例 1:
输入: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] 输出: 5 解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。示例 2:
输入: beginWord = "hit" endWord = "cog" wordList = ["hot","dot","dog","lot","log"] 输出: 0 解释: endWord "cog" 不在字典中,所以无法进行转换。
代码
from collections import deque
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
word_set = set(wordList)
if len(word_set)==0 or endWord not in word_set:
return 0
if beginWord in word_set:
word_set.remove(beginWord)
visited = set()
visited.add(beginWord)
visited.add(endWord)
begin_visited = set()
begin_visited.add(beginWord)
end_visited = set()
end_visited.add(endWord)
word_len = len(beginWord)
step = 1
while begin_visited:
if len(begin_visited) > len(end_visited):
begin_visited, end_visited = end_visited, begin_visited
next_level_visited = set()
for word in begin_visited:
word_list = list(word)
for j in range(word_len):
origin_char = word_list[j]
for k in range(26):
word_list[j] = chr(ord('a')+k)
next_word = ''.join(word_list)
if next_word in word_set:
if next_word in end_visited:
return step+1
if next_word not in visited:
next_level_visited.add(next_word)
visited.add(next_word)
word_list[j] = origin_char
begin_visited = next_level_visited
step+=1
return 0
11.4
哎,今天考完了操作系统
虽然基本都是原题,但是有道15分的甘特图我估计🈚了
题目
57. 插入区间
难度困难
给出一个*无重叠的 ,*按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
示例 1:
输入:intervals = [[1,3],[6,9]], newInterval = [2,5] 输出:[[1,5],[6,9]]示例 2:
输入:intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8] 输出:[[1,2],[3,10],[12,16]] 解释:这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
困难题就这
不过是多写几个elif的事情
不说了,复习计算机网络去了

代码
class Solution:
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
if len(intervals)==0:
return [newInterval]
tmp = []
new_left, new_right = newInterval[0], newInterval[1]
if new_right<intervals[0][0]:
return [newInterval]+intervals
if new_left>intervals[-1][1]:
return intervals+[newInterval]
flag = False
for i in range(len(intervals)):
left, right = intervals[i][0], intervals[i][1]
if new_left<=left and new_right>=right:
# 第一种情况newInterval包含了[left, right]
tmp.append(newInterval)
flag = True
elif left<=new_left and right>=new_right:
tmp.append(intervals[i])
flag = True
elif new_left<=right and new_right>=right:
tmp.append([left, new_right])
flag = True
elif new_left<=left and new_right>=left:
tmp.append([new_left, right])
flag = True
else:
tmp.append(intervals[i])
if not flag:
# 说明没插入
for i in range(len(tmp)-1):
if tmp[i+1][0]>new_right:
tmp = tmp[:i+1]+[newInterval]+tmp[i+1:]
# 合并有重叠的数组
if len(tmp) == 1:
return tmp
ans = []
i = 0
while i<len(tmp)-1:
left1, right1 = tmp[i]
left2, right2 = tmp[i+1]
if right1<left2:
ans.append(tmp[i])
else:
while i<len(tmp)-1 and tmp[i+1][0]<=right1:
i += 1
# 这个时候找到了需要合并的右边界
ans.append([left1,tmp[i][1]])
i += 1
if i==len(tmp)-1:
ans.append(tmp[-1])
break
return ans
11.3
题目
941. 有效的山脉数组
难度简单
给定一个整数数组
A,如果它是有效的山脉数组就返回true,否则返回false。让我们回顾一下,如果 A 满足下述条件,那么它是一个山脉数组:
A.length >= 3在
0 < i < A.length - 1条件下,存在
i使得:
A[0] < A[1] < ... A[i-1] < A[i]
A[i] > A[i+1] > ... > A[A.length - 1]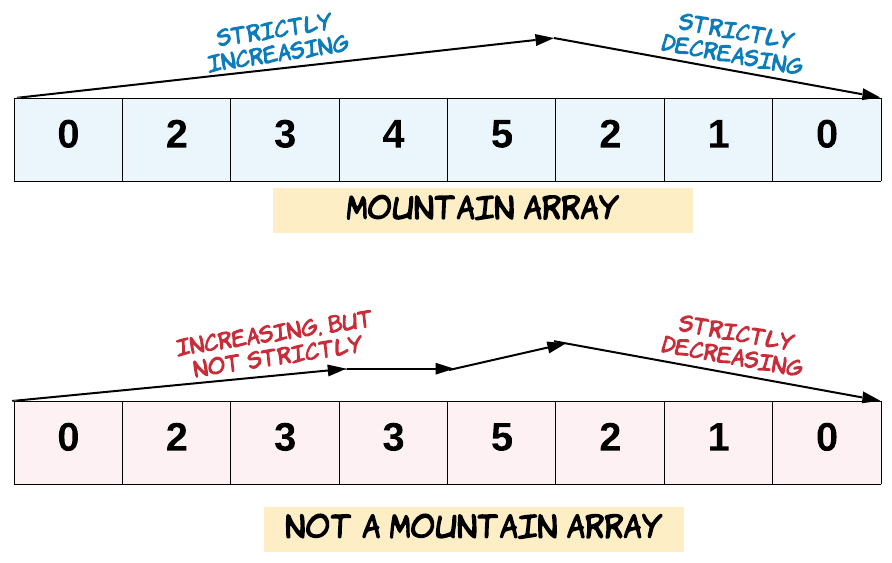
示例 1:
输入:[2,1] 输出:false示例 2:
输入:[3,5,5] 输出:false示例 3:
输入:[0,3,2,1] 输出:true提示:
0 <= A.length <= 100000 <= A[i] <= 10000
代码
class Solution:
def validMountainArray(self, A: List[int]) -> bool:
if len(A)<3:
return False
prev = A[0]-1 # 用来记录经过的上一个数
flag = 0 # 用来记录是否已经翻过山峰
for i in A:
if flag==0 and i>prev:
prev = i
elif flag==0 and i<prev and i!=A[0]-1:
flag = 1
prev = i
elif flag == 1 and i<prev:
prev = i
else:
return False
if flag == 1:
return True
else:
return False
11.2
软件测试的期中考试有点崩,sad
近日只贴代码
题目
349. 两个数组的交集
难度简单
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2] 输出:[2]示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4] 输出:[9,4]说明:
- 输出结果中的每个元素一定是唯一的。
- 我们可以不考虑输出结果的顺序。
代码
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
if len(nums1)>len(nums2):
nums1, nums2 = nums2, nums1
ans = []
for i in set(nums1):
if i in nums2:
ans.append(i)
return ans
赶紧复习操作系统和计网去了,想保住3.9好难TAT
11.1
刚刚竟然没注意把日期写成了10.32🙃
估计是学傻了
可惜了昨天的sn没能夺冠(dwg就nm强得离谱)
题目
140. 单词拆分 II
难度困难
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,在字符串中增加空格来构建一个句子,使得句子中所有的单词都在词典中。返回所有这些可能的句子。
说明:
- 分隔时可以重复使用字典中的单词。
- 你可以假设字典中没有重复的单词。
示例 1:
输入: s = "catsanddog" wordDict = ["cat", "cats", "and", "sand", "dog"] 输出: [ "cats and dog", "cat sand dog" ]示例 2:
输入: s = "pineapplepenapple" wordDict = ["apple", "pen", "applepen", "pine", "pineapple"] 输出: [ "pine apple pen apple", "pineapple pen apple", "pine applepen apple" ] 解释: 注意你可以重复使用字典中的单词。示例 3:
输入: s = "catsandog" wordDict = ["cats", "dog", "sand", "and", "cat"] 输出: []
思路
我一开始看到这题目还很开心,因为在一节专选课刚做过分词法的实验
可惜最大前向匹配法和最大后相匹配法并不能解决这个问题,因为从这里的示例二就能看出来,他的分词不是用“最大”这个规则能解决的
单纯地使用前向或后向并不能把pineapple拆解成pine apple
咋办呢,看大佬题解呗
- 动态规划+dfs
- 用动态规划求解字符的前n个字符能否拆解成若干字串
- 用一个dp数组去记录
- 用dfs,在dp数组的基础上,去找到所有可能性
就写个大概思路吧,还要准备三门专业必修课的期中考试😭

