12.31

再见啦，2020

太困了，先睡一会儿

题目

435. 无重叠区间

难度中等271

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

1. 可以认为区间的终点总是大于它的起点。
2. 区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

示例 1:

输入: [ [1,2], [2,3], [3,4], [1,3] ]

输出: 1

解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: [ [1,2], [1,2], [1,2] ]

输出: 2

解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

输入: [ [1,2], [2,3] ]

输出: 0

解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

代码

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        # 贪心
        if len(intervals)<2: return 0
        intervals.sort(key = lambda x:x[1])
        last_end = intervals[0][1]
        cnt = 1
        for left, right in intervals[1:]:
            if left>=last_end:
                cnt += 1
                last_end = right
        return len(intervals)-cnt

12.30

题目

1046. 最后一块石头的重量

难度简单

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出两块 最重的 石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下，就返回 0。

示例：

输入：[2,7,4,1,8,1]
输出：1
解释：
先选出 7 和 8，得到 1，所以数组转换为 [2,4,1,1,1]，
再选出 2 和 4，得到 2，所以数组转换为 [2,1,1,1]，
接着是 2 和 1，得到 1，所以数组转换为 [1,1,1]，
最后选出 1 和 1，得到 0，最终数组转换为 [1]，这就是最后剩下那块石头的重量。

提示：

1. 1 <= stones.length <= 30
2. 1 <= stones[i] <= 1000

代码

import heapq
class Solution:
    def lastStoneWeight(self, stones: List[int]) -> int:
        stones = [-i for i in stones]
        heapify(stones)
        while len(stones)>1:
            big, small = -heapq.heappop(stones), -heapq.heappop(stones)
            if big==small:
                continue
            else:
                heapq.heappush(stones, -(big-small))
        return 0 if not len(stones) else -heapq.heappop(stones)

12.29

老样子，期末考试期间不写题解

题目

330. 按要求补齐数组

难度困难

给定一个已排序的正整数数组 *nums，*和一个正整数 *n 。*从 [1, n] 区间内选取任意个数字补充到 nums 中，使得 [1, n] 区间内的任何数字都可以用 nums 中某几个数字的和来表示。请输出满足上述要求的最少需要补充的数字个数。

示例 1:

输入: nums = [1,3], n = 6
输出: 1 
解释:
根据 nums 里现有的组合 [1], [3], [1,3]，可以得出 1, 3, 4。
现在如果我们将 2 添加到 nums 中， 组合变为: [1], [2], [3], [1,3], [2,3], [1,2,3]。
其和可以表示数字 1, 2, 3, 4, 5, 6，能够覆盖 [1, 6] 区间里所有的数。
所以我们最少需要添加一个数字。

示例 2:

输入: nums = [1,5,10], n = 20
输出: 2
解释: 我们需要添加 [2, 4]。

示例 3:

输入: nums = [1,2,2], n = 5
输出: 0

代码

class Solution:
    def minPatches(self, nums: List[int], n: int) -> int:
        res, x = 0, 1
        index, length = 0, len(nums)
        while x<=n:
            if index<len(nums) and nums[index]<=x:
                x += nums[index]
                index += 1
            else:
                x *= 2
                res += 1
        return res

12.28

题目

188. 买卖股票的最佳时机 IV

难度困难

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

**注意：**你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：

输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
     随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

提示：

• 0 <= k <= 10^9
• 0 <= prices.length <= 1000
• 0 <= prices[i] <= 1000

思路

动态规划

又是复习，参考着大佬的代码优化了一下

代码

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        # 动态规划
        # 开辟两个数组，一个存放当天结束时候没有股票，另一个存放当天结束的时候手里有股票
        buy = [-float('inf') for i in range(k+1)]
        sell = [0 for i in range(k+1)]
        for price in prices:
            for j in range(1,k+1):
                buy[j] = max(sell[j-1]-price, buy[j])
                sell[j] = max(sell[j], buy[j]+price)
        return sell[k]

12.27

题目

205. 同构字符串

难度简单282

给定两个字符串 s 和 *t*，判断它们是否是同构的。

如果 s 中的字符可以被替换得到 *t* ，那么这两个字符串是同构的。

所有出现的字符都必须用另一个字符替换，同时保留字符的顺序。两个字符不能映射到同一个字符上，但字符可以映射自己本身。

示例 1:

输入: s = "egg", t = "add"
输出: true

示例 2:

输入: s = "foo", t = "bar"
输出: false

示例 3:

输入: s = "paper", t = "title"
输出: true

思路

用两个字典互相映射

代码

class Solution:
    def isIsomorphic(self, s: str, t: str) -> bool:
        dic_s, dic_t = dict(), dict()
        for i in range(len(s)):
            cur_s, cur_t = s[i], t[i]
            if cur_s in dic_s and dic_s[cur_s] != cur_t:
                return False
            if cur_t in dic_t and dic_t[cur_t] != cur_s:
                return False
            dic_s[cur_s] = cur_t
            dic_t[cur_t] = cur_s
        return True

12.26

题目

85. 最大矩形

难度困难

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [["0"]]
输出：0

示例 4：

输入：matrix = [["1"]]
输出：1

示例 5：

输入：matrix = [["0","0"]]
输出：0

提示：

• rows == matrix.length
• cols == matrix[0].length
• 0 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

思路

就算是困难题，也给你锤烂，暴力法，yyds！（其实就是自己菜）

1. 暴力解法

   为了确定每个位置能扩展出来最大的矩形面积，我们要知道这个位置向右有多少个连续的1，向下有多少个连续的1。知道之后呢，就分别向右和向下遍历，确定矩形的最大面积即可。

   以向下遍历为例，假设当前这个位置向右有5个连续的1

   • 我们初始化宽度为5，高度为1，当前的最大矩形面积是5
   • 开始向下遍历
     • 向下一格之后，数字是1，向右最多有4个连续的1，因此当前宽度就只能是4，高度为2，最大矩形面积为8
     • 再向下一格，数字是1，向右最多有3个连续的1，当前宽度就是3，高度为3，最大面积9
     • 再向下一格，数字是0，因此停止扩展
   • 向右遍历也是一个道理

2. 递增栈的巧妙解法

   算法详情84. 柱状图中最大的矩形

   首先初始化一个高度数组heights，去记录每列最多有多少个连续的1

   按行去遍历数组，以题目里的例子为例

   
   • 第一行的时候 heights = [1,0,1,0,0]
   • 第二行的时候 heights = [2,0,2,1,1]
   • 第三行的时候 heights = [3,1,2,2,2]
   • 以第三行为例，来当前情况下求最大的面积
   • 为了减少判断，我们往数组里放两个哨兵 heights = [0]+heights+[0]
   • 初始化递增栈 stk=[0]
   • 从j=1开始遍历 heights
     • 当前的heights[j]=3比栈顶位置的高度heights[stk[-1]]=0高，所以直接把j丢到栈里
     • 当前的heights[j]=1比栈顶位置的高度3要小，所以我们当前就能确定以3为高度的最大矩形面积
     • 我们把栈顶元素pop出来，它的位置是1，因为我们的栈是递增栈，所以当前栈里的所有元素的位置的高度必定是比3要小的，所以我们的宽度只能是当前遍历的位置2减去栈顶元素的位置0再减去1，乘上高度3，所以最大面积就是3
     • 之后同理

俺只是抄题解的菜🐓罢了

代码

1. 暴力

   class Solution:
       def maximalRectangle(self, matrix: List[List[str]]) -> int:
           rows = len(matrix)
           if not matrix:
               return 0
           cols = len(matrix[0])
           # 记录每个1的右边和下边最多有多少个连续的1
           # 先记录行
           for i in range(rows-1,-1,-1):
               last = 0
               for j in range(cols-1,-1,-1):
                   if matrix[i][j] =='1':
                       last += 1
                       matrix[i][j] = ['1', last]
                   else:
                       last = 0
           for j in range(cols-1,-1,-1):
               last = 0 
               for i in range(rows-1,-1,-1):
                   if matrix[i][j][0] == '1':
                       last += 1
                       matrix[i][j].append(last)
                   else:
                       last = 0
           res = 0
           for i in range(rows):
               for j in range(cols):
                   if matrix[i][j][0]=='1':
                       # 向下找到最大的扩展可能性
                       height = 1
                       width = matrix[i][j][1]
                       row, col = i, j
                       res = max(res, height*width)
                       while row+1<rows and matrix[row+1][j][0]=='1':
                           row += 1
                           height += 1
                           width = min(width, matrix[row][j][1])
                           res = max(width*height, res)
                       # 再向右找到最大的扩展可能性
                       width = 1
                       height = matrix[i][j][2]
                       while col+1<cols and matrix[i][col+1][0]=='1':
                           col += 1
                           width += 1
                           height = min(height, matrix[row][j][2])
                           res = max(width*height, res)
           return res
   

2. 借助递增栈

   class Solution:
       def maximalRectangle(self, matrix: List[List[str]]) -> int:
           rows = len(matrix)
           if not matrix:
               return 0
           cols = len(matrix[0])
           # 每次按列记录上面有多少个连续的1
           res = 0
           heights = [0 for i in range(cols+2)] # 加入了两哨兵站
           for i in range(rows):
               for j in range(cols):
                   if matrix[i][j] == '1':
                       heights[j+1] += 1
                   else:
                       heights[j+1] = 0
               # 更新完heights数组之后开始求最大面积
               stk = [0] # stk是一个递增栈
               for j in range(1,cols+2):
                   while heights[j] < heights[stk[-1]]:
                       index = stk.pop()
                       width = j-(stk[-1]+1)
                       res = max(res, width*heights[index])
                   stk.append(j)
           return res
   

12.25

题目

455. 分发饼干

难度简单

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示：

• 1 <= g.length <= 3 * 104
• 0 <= s.length <= 3 * 104
• 1 <= g[i], s[j] <= 231 - 1

思路

双指针

先对胃口数组和饼干数组排序，升序

然后分别用i,j两个指针遍历数组，如果胃口大，就把饼干数组的指针右移直到能吃饱为止

代码

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()
        s.sort()
        i, j, res = 0, 0, 0
        while i<len(g) and j<len(s):
            while j<len(s) and g[i]>s[j]:
                j += 1
            if j<len(s):
                i += 1
                j += 1
                res += 1
        return res

12.24

这就是困难题吗，莫名其妙过了，爱了爱了

题目

135. 分发糖果

难度困难

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。
• 相邻的孩子中，评分高的孩子必须获得更多的糖果。

那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1:

输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。

示例 2:

输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

思路

• 先从左向右遍历，保证单方面合理
  • 如果当前遍历的孩子的评分比左侧的分数高
  • 我给他的糖果数就要比左侧的孩子多一个
• 再从右向左遍历，保证双方面合理
  • 如果当前遍历的孩子的评分比右侧的分数高
  • 我给他的糖果数就要比右侧的孩子多一个
  • 在这次遍历决定糖果数的时候要保证，当前的糖果数不能比之前单方面考虑的时候少

我也不知道为什么这么纯粹的贪心就 AC 了

代码

class Solution:
    def candy(self, ratings: List[int]) -> int:
        if not ratings:
            return 0
        n = len(ratings)
        candy = [1 for i in range(n)]
        for i in range(1,len(ratings)):
            if ratings[i]>ratings[i-1]:
                candy[i] = candy[i-1]+1
        for i in range(len(ratings)-2,-1,-1):
            if ratings[i]>ratings[i+1]:
                candy[i] = max(candy[i+1]+1, candy[i]) 
        return sum(candy)

12.23

我可太困了😴

题目

387. 字符串中的第一个唯一字符

难度简单

给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。

示例：

s = "leetcode"
返回 0

s = "loveleetcode"
返回 2

思路

• 哈希表计数
• 找到所有出现次数为1的字母
• 找到这些字母中位置最靠前的

代码

class Solution:
    def firstUniqChar(self, s: str) -> int:
        dic = dict()
        for i in s:
            if i in dic:
                dic[i] += 1
            else:
                dic[i] = 1
        res = []
        for i in set(s):
            if dic[i] == 1:
                res.append(s.index(i))
        return min(res) if res else -1     

12.22

为啥层序遍历也变成中等难度了🧐

题目

103. 二叉树的锯齿形层序遍历

难度中等

给定一个二叉树，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如： 给定二叉树 [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回锯齿形层序遍历如下：

[
  [3],
  [20,9],
  [15,7]
]

思路

层序遍历，根据当前遍历的层数来决定是否要倒序输出

代码

class Solution:
    def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        nodes, res = [],[]
        nodes.append(root)
        height = 0
        while nodes:
            tmp, cur = [],[]
            for node in nodes:
                cur.append(node.val)
                if node.left:
                    tmp.append(node.left)
                if node.right:
                    tmp.append(node.right)
            if height%2==0:
                res.append(cur)
            else:
                res.append(cur[::-1])
            height += 1
            nodes = tmp
        return res

12.21

easy cozy

题目

746. 使用最小花费爬楼梯

难度简单436

数组的每个索引作为一个阶梯，第 i个阶梯对应着一个非负数的体力花费值 cost[i](索引从0开始)。

每当你爬上一个阶梯你都要花费对应的体力花费值，然后你可以选择继续爬一个阶梯或者爬两个阶梯。

您需要找到达到楼层顶部的最低花费。在开始时，你可以选择从索引为 0 或 1 的元素作为初始阶梯。

示例 1:

输入: cost = [10, 15, 20]
输出: 15
解释: 最低花费是从cost[1]开始，然后走两步即可到阶梯顶，一共花费15。

示例 2:

输入: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出: 6
解释: 最低花费方式是从cost[0]开始，逐个经过那些1，跳过cost[3]，一共花费6。

注意：

1. cost 的长度将会在 [2, 1000]。
2. 每一个 cost[i] 将会是一个Integer类型，范围为 [0, 999]。

思路

最纯粹的动态规划，唯一的小trick就是在原数组后面加个0

真的搞不懂为啥设定成最后一级台阶不是楼顶

代码

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        n = len(cost)
        cost.append(0)
        dp = [0 for i in range(n+1)]
        dp[0], dp[1] = cost[0], cost[1]
        for i in range(2, len(cost)):
            dp[i] = min(dp[i-1], dp[i-2])+cost[i]
        return dp[-1]

12.20

题目

316. 去除重复字母

难度中等

给你一个字符串 s ，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证 返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

示例 1：

输入：s = "bcabc"
输出："abc"

示例 2：

输入：s = "cbacdcbc"
输出："acdb"

提示：

• 1 <= s.length <= 104
• s 由小写英文字母组成

思路

• 边遍历s，边考虑我们要保留哪些字母，丢弃哪些字母

• 用一个栈去存储我们选择保留的字母

• 假设当前遍历的是s

  • 如果s已经在栈中，就忽略

  • 否则就保留s

  • 但是为了最后的输出字典序最小，我们需要尽可能地删掉和s相邻且比s还要大的字母

  • 在删除的同时，还要保证不能太贪了，如果要准备删的字母是它最后一次出现了，就停手

  感觉有点像满门抄斩，但是给留个独苗

代码

class Solution:
    def removeDuplicateLetters(self, s: str) -> str:
        dic = collections.Counter(s)
        res = []
        for i in s:
            if i not in res:
                while res and res[-1]>i and dic[res[-1]]>0:
                    res.pop()
                res.append(i)
            dic[i] -= 1
        return "".join(res)

12.19

题目

48. 旋转图像

难度中等

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在**原地**旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

思路

好家伙，给我人转晕了，我们慢慢分析，找一下规律

• 假设矩阵行数=n，列数=n
  • 以第二个矩阵为例，行数=4，列数=4，经过旋转
  • (1,0)=>(0,2)
  • (1,1)=>(1,2)
  • (1,2)=>(2,2)
  • (1,3)=>(3,1)
• 矩阵中的(row,col)在旋转90°之后，到了(col,n-row-1)
  • 即(row,col)=>(col,n-row-1)
• 根据这个规律可以有两种实现矩阵原地旋转的方式

1. 设缓存量，逐个交换

   每次的旋转都可以把元素分成四个一组，将四个元素的值逐个交换

   这四个元素分别是

   • matrix[row][col]
   • matrix[col,n-row-1]
   • matrix[n-row-1,n-col-1]
   • matrix[n-col-1,row]

   只要让第一个值到第二个位置去，第二个值到第三个位置去，第三个值到第四个位置去，第四个值到第一个位置去即可

   要实现这个，可以设一个缓存量tmp，来实现四个元素的值的交换（python也可以直接交换，但是我个人觉得代码可读性太差了）

   还有一个问题是应该分成哪些组呢？

   偶数情况就是平均分成四块，n^2 = 4*(n/2)*(n/2)

   奇数情况需要分解成n^2 = 4*((n-1)/2)*((n+1)/2)+1直接看官方题解的图吧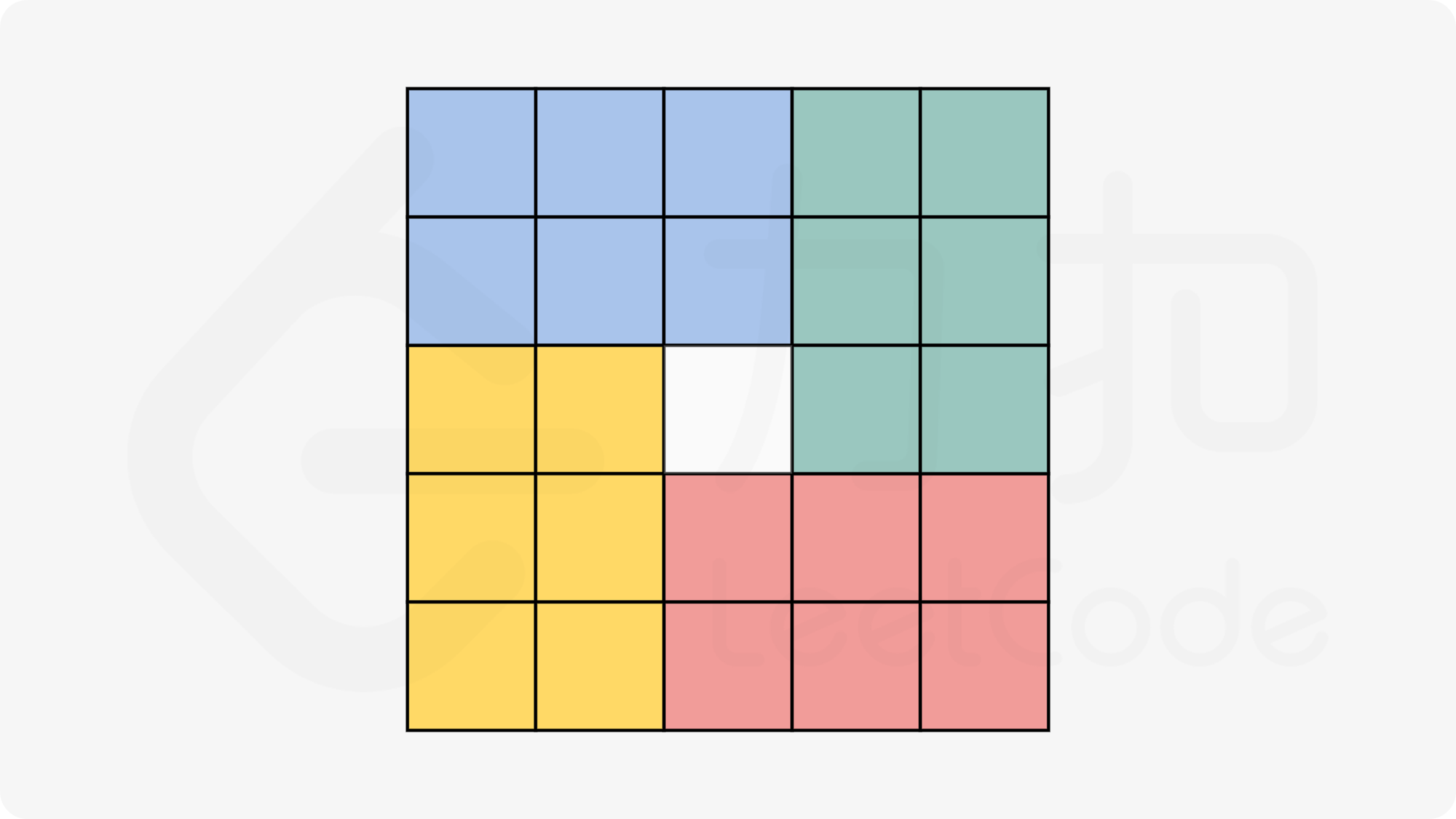

   

2. 巧翻转

   首先将矩阵按水平轴翻转，即上下翻转

   matrix[row][col]=matrix[n-row-1][col]

   再将矩阵根据主对角线翻转，即右上的元素到左下

   matrix[n-row-1][col]=matrix[col][n-row-1]

   因此最后实现的是

   matrix[row][col]=>matrix[col][n-row-1]

   正好是我们要求的变换

代码

1. 逐个交换

   class Solution:
       def rotate(self, matrix: List[List[int]]) -> None:
           """
           Do not return anything, modify matrix in-place instead.
           """
           n = len(matrix)
           for i in range(n//2):
               for j in range((n+1)//2):
                   tmp = matrix[i][j]
                   matrix[i][j] = matrix[n-j-1][i]
                   matrix[n-j-1][i] = matrix[n-i-1][n-j-1]
                   matrix[n-i-1][n-j-1] = matrix[j][n-i-1]
                   matrix[j][n-i-1] = tmp
   

2. 翻转

   class Solution:
       def rotate(self, matrix: List[List[int]]) -> None:
           """
           Do not return anything, modify matrix in-place instead.
           """
           n = len(matrix)
           # 上下翻转
           for i in range(n//2):
               for j in range(n):
                   matrix[i][j], matrix[n-i-1][j] = matrix[n-i-1][j], matrix[i][j]
           # 对角线翻转
           for i in range(n):
               for j in range(i):
                   matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
   

12.18

题目

389. 找不同

难度简单

给定两个字符串 s 和 t，它们只包含小写字母。

字符串 *t* 由字符串 *s* 随机重排，然后在随机位置添加一个字母。

请找出在 t 中被添加的字母。

示例 1：

输入：s = "abcd", t = "abcde"
输出："e"
解释：'e' 是那个被添加的字母。

示例 2：

输入：s = "", t = "y"
输出："y"

示例 3：

输入：s = "a", t = "aa"
输出："a"

示例 4：

输入：s = "ae", t = "aea"
输出："a"

提示：

• 0 <= s.length <= 1000
• t.length == s.length + 1
• s 和 t 只包含小写字母

思路

哈，都可以哈

用一个字典统计字母出现次数，s中出现了就-1，t出现了就+1

最后value为1对应的key就是我们要找的字母

代码

from collections import defaultdict
class Solution:
    def findTheDifference(self, s: str, t: str) -> str:
        dic_t = defaultdict(int)
        for i in t:
            dic_t[i] += 1
        for i in s:
            dic_t[i] -= 1
        for i in dic_t.keys():
            if dic_t[i]>0:
                return i

12.17

正好复习一下两个星期前看的labuladong的算法小抄

题目

714. 买卖股票的最佳时机含手续费

难度中等

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

**注意：**这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1:

输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:  
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

注意:

• 0 < prices.length <= 50000.

• 0 < prices[i] < 50000.

• 0 <= fee < 50000.

思路

动态规划三要素

1. dp数组定义

   因为我们每天结束的时候最多两个状态

   • 手里没股票
   • 手里有股票

   所以就定义

   • dp[i][0]表示第i天结束的时候手里没股票时的最大利润

   • dp[i][1]表示第i天结束的时候手里有股票时的最大利润

2. base case

   一开始每天的利润初始化为0

   根据数组定义，第0天的状态就是dp[0][0]=0,dp[0][1]=-prices[0]

3. 状态转移方程

   如果当天结束的时候没有股票，有两种可能

   • 当天卖出了股票
   • 当天开始的时候就没有股票

   如果当天结束的时候有股票

   • 当天新买的股票
   • 当天开始的时候已经持有了股票

   因此，考虑到手续费，状态转移方程为

   dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i]-fee)

   dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])

代码

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        # 动态规划
        n = len(prices)
        dp = [[0,0] for i in range(n)]
        # base case
        dp[0][0], dp[0][1] = 0, -prices[0]
        for i in range(1,n):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i]-fee)
            dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
        return max(dp[-1][0], dp[-1][1])

优化一下空间

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        # 动态规划
        n = len(prices)
        dp = [[0,0] for i in range(n)]
        # base case
        dp0, dp1 = 0, -prices[0]
        for i in range(1,n):
            dp0, dp1 = max(dp0, dp1+prices[i]-fee), max(dp1, dp0-prices[i])
        return max(dp0, dp1)

12.16

题目

290. 单词规律

难度简单237

给定一种规律 pattern 和一个字符串 str ，判断 str 是否遵循相同的规律。

这里的 遵循 指完全匹配，例如， pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应规律。

示例1:

输入: pattern = "abba", str = "dog cat cat dog"
输出: true

示例 2:

输入:pattern = "abba", str = "dog cat cat fish"
输出: false

示例 3:

输入: pattern = "aaaa", str = "dog cat cat dog"
输出: false

示例 4:

输入: pattern = "abba", str = "dog dog dog dog"
输出: false

说明: 你可以假设 pattern 只包含小写字母， str 包含了由单个空格分隔的小写字母。

思路

两个哈希表互相找，一个以pattern中的字母为key，一个以str中的单词为key

代码

class Solution:
    def wordPattern(self, pattern: str, s: str) -> bool:
        dic_p = dict()
        dic_w = dict()
        words = s.split(" ")
        if len(words) != len(pattern):
            return False
        for i in range(len(words)):
            p = pattern[i]
            w = words[i]
            if p not in dic_p and w not in dic_w:
                dic_p[p] = w
                dic_w[w] = p
            elif p not in dic_p or w not in dic_w:
                return False
            else:
                if dic_p[p] != w or dic_w[w]!=p:
                    return False
        return True

12.15

题目

738. 单调递增的数字

难度中等

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）

示例 1:

输入: N = 10
输出: 9

示例 2:

输入: N = 1234
输出: 1234

示例 3:

输入: N = 332
输出: 299

说明: N 是在 [0, 10^9] 范围内的一个整数。

思路

用递增栈存数字，然后贪！

我们首先来找一下思路

1. 如果原来的数字能顺利的存放到递增栈中，那挺好，直接返回就行。

2. 但是大部分情况下都不是这样的，例如3455521，它在第6位，即2开始不是递增的了，这个时候该怎么办呢？

   这个时候肯定应该丢掉栈顶的一部分数字，然后把栈顶的一个数字减小1，来保证我最后的结果比原数字小。

   然后放尽可能多的9到栈里，来保证最后我的结果最大。

OK，现在来思考要丢掉几个数字，放几个9

• 可以看到，当我尝试放2的时候，我的栈应该是[3, 4, 5, 5, 5]
• 这个时候，如果只丢掉一个5，就变成[3, 4, 5, 5]，这个时候把栈顶元素减小1，那就不是递增的了呀
• 所以我们要让栈顶丢到只剩一个5，然后把5变成4放到栈里面去
• 再补9，9的个数应该是当前原数字的长度减掉当前栈的长度

代码

class Solution:
    def monotoneIncreasingDigits(self, N: int) -> int:
        # 贪心法
        N = str(N)
        res = []
        for i in range(len(N)):
            if not res or int(N[i])>=int(res[-1]):
                res.append(N[i])
                continue
            while len(res)>=2 and res[-1]==res[-2]:
                res.pop()
            if int(res[-1])>0:
                res[-1] = str(int(res[-1])-1)
            else:
                res.pop()
            while len(res)<len(N):
                res.append('9')
            break
        return int(''.join(res))

12.14

昨天csp熬了三个多小时才200多分 💢

题目

49. 字母异位词分组

难度中等

给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。

示例:

输入: ["eat", "tea", "tan", "ate", "nat", "bat"]
输出:
[
  ["ate","eat","tea"],
  ["nat","tan"],
  ["bat"]
]

说明：

• 所有输入均为小写字母。
• 不考虑答案输出的顺序。

思路

无非就是建一个字典，定义一个key，然后把所有字母异位词放到一个value里。

1. 手动哈希

   把所有的字符串转换成自定义的键值

   例如“sssdda”我就转换成“a1d2s3”，这样就可以很方便地存取

2. 排序

   所有字符串都按字母序排一遍序，这样子字母异位词就是同一个词了

   事实证明排序比上面第一种方法快得多

​ 排序🐂🍺嗷

代码

1. 哈希

class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        # 手动哈希
        dic = dict()
        words = 'abcdefghijklmnopqrstuvwxyz'
        for word in strs:
            hash_code = ""
            for w in words:
                if word.count(w)>0:
                    hash_code += w+str(word.count(w))
            if hash_code in dic:
                dic[hash_code].append(word)
            else:
                dic[hash_code] = [word]
        return list(dic.values())

2. 排序

class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        # 排序
        dic = dict()
        for word in strs:
            hash_code = "".join(sorted(word))
            if hash_code in dic:
                dic[hash_code].append(word)
            else:
                dic[hash_code] = [word]
        return list(dic.values())

12.13

嚯，今天考csp，leetcode竟然给我放假

题目

217. 存在重复元素

难度简单

给定一个整数数组，判断是否存在重复元素。

如果任意一值在数组中出现至少两次，函数返回 true 。如果数组中每个元素都不相同，则返回 false 。

示例 1:

输入: [1,2,3,1]
输出: true

示例 2:

输入: [1,2,3,4]
输出: false

示例 3:

输入: [1,1,1,3,3,4,3,2,4,2]
输出: true

思路

• 哈希表

代码

class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        return len(nums)!=len(set(nums))

12.12

美好的周末从看题解开始

题目

376. 摆动序列

难度中等

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为**摆动序列。**第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例 1:

输入: [1,7,4,9,2,5]
输出: 6 
解释: 整个序列均为摆动序列。

示例 2:

输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。

示例 3:

输入: [1,2,3,4,5,6,7,8,9]
输出: 2

进阶: 你能否用 O(n) 时间复杂度完成此题

思路

动态规划

• 建立两个数组up,down

• up[i],down[i]分别表示nums的前i个数字能够组成的最长子序列长度

• 其中up数组存储的子序列要求最后是上升的，down数组的子序列最后是下降的

• base case

  • up[0], down[0] = 1, 1

• 状态转移

  

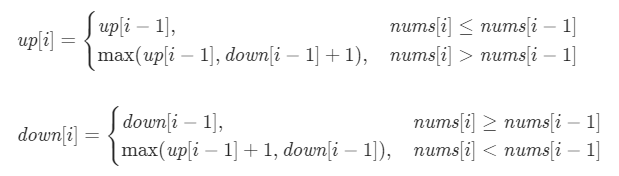
• 最后比较这两个数组中的最后一个值，大的那个就是答案

代码

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        n = len(nums)
        if not nums:
            return 0
        up = [0 for i in range(n)]
        down = [0 for i in range(n)]
        # 这两个数组用来记录遍历到i时的最大子序列长度
        up[0], down[0] = 1, 1
        for i in range(1,n):
            if nums[i]<nums[i-1]:
                up[i] = up[i-1]
                down[i] = max(down[i-1], up[i-1]+1)
            elif nums[i]>nums[i-1]:
                up[i] = max(down[i-1]+1, up[i-1])
                down[i] = down[i-1]
            else:
                up[i] = up[i-1]
                down[i] = down[i-1]
        return max(down[n-1], up[n-1])

12.11

题目

649. Dota2 参议院

难度中等

Dota2 的世界里有两个阵营：Radiant(天辉)和 Dire(夜魇)

Dota2 参议院由来自两派的参议员组成。现在参议院希望对一个 Dota2 游戏里的改变作出决定。他们以一个基于轮为过程的投票进行。在每一轮中，每一位参议员都可以行使两项权利中的**一**项：

1. 禁止一名参议员的权利：

   参议员可以让另一位参议员在这一轮和随后的几轮中丧失所有的权利。

2. 宣布胜利：

​ 如果参议员发现有权利投票的参议员都是同一个阵营的，他可以宣布胜利并决定在游戏中的有关变化。

给定一个字符串代表每个参议员的阵营。字母 “R” 和 “D” 分别代表了 Radiant（天辉）和 Dire（夜魇）。然后，如果有 n 个参议员，给定字符串的大小将是 n。

以轮为基础的过程从给定顺序的第一个参议员开始到最后一个参议员结束。这一过程将持续到投票结束。所有失去权利的参议员将在过程中被跳过。

假设每一位参议员都足够聪明，会为自己的政党做出最好的策略，你需要预测哪一方最终会宣布胜利并在 Dota2 游戏中决定改变。输出应该是 Radiant 或 Dire。

示例 1：

输入："RD"
输出："Radiant"
解释：第一个参议员来自 Radiant 阵营并且他可以使用第一项权利让第二个参议员失去权力，因此第二个参议员将被跳过因为他没有任何权利。然后在第二轮的时候，第一个参议员可以宣布胜利，因为他是唯一一个有投票权的人

示例 2：

输入："RDD"
输出："Dire"
解释：
第一轮中,第一个来自 Radiant 阵营的参议员可以使用第一项权利禁止第二个参议员的权利
第二个来自 Dire 阵营的参议员会被跳过因为他的权利被禁止
第三个来自 Dire 阵营的参议员可以使用他的第一项权利禁止第一个参议员的权利
因此在第二轮只剩下第三个参议员拥有投票的权利,于是他可以宣布胜利

提示：

• 给定字符串的长度在 [1, 10,000] 之间.

思路

双队列模拟投票即可，好困，睡了

代码

class Solution:
    def predictPartyVictory(self, senate: str) -> str:
        senate_r, senate_d = [], []
        n = len(senate)
        for i in range(n):
            if senate[i] == 'D':
                senate_d.append(i)
            else:
                senate_r.append(i)
        while senate_r and senate_d:
            if senate_r[0] < senate_d[0]:
                senate_r.append(senate_r[0]+n)
            else:
                senate_d.append(senate_d[0]+n)
            senate_d.pop(0)
            senate_r.pop(0)
        if senate_r: return "Radiant"
        else: return "Dire"

12.10

题目

860. 柠檬水找零

难度简单

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。

顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例 1：

输入：[5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。

示例 2：

输入：[5,5,10]
输出：true

示例 3：

输入：[10,10]
输出：false

示例 4：

输入：[5,5,10,10,20]
输出：false
解释：
前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。

提示：

• 0 <= bills.length <= 10000
• bills[i] 不是 5 就是 10 或是 20

思路

经典老番，模拟即可

代码

class Solution:
    def lemonadeChange(self, bills: List[int]) -> bool:
        dic = dict()
        dic[5], dic[10] = 0, 0
        for i in bills:
            if i == 5:
                dic[5] += 1
            elif i == 10:
                if dic[5]==0:
                    return False
                else:
                    dic[5] -= 1
                    dic[10] += 1
            else:
                if dic[10]>0 and dic[5]>0:
                    dic[10] -=1
                    dic[5]-=1
                elif dic[5]>=3:
                    dic[5] -=3
                else:
                    return False
        return True

12.9

题目

62. 不同路径

难度中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

思路

蛮经典的题目，一开始直接套递归，结果超时了

动态规划轻松ac

• 定义dp数组

  • dp[i][j]代表了从0,0到i,j有多少种走法

• 状态转移

  • 因为只能向下走或者向右走，所以每格的走法就是上面一格的走法加左边一格的走法
  • dp[i][j]=dp[i-1][j]+dp[i][j-1]

• base case

  • 将dp[0,0]定义为1，因为我们从起点出发，就一种走法

• 遍历更新整个dp数组即可，最后dp[m-1][n-1]就是我们的答案

代码

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        paths = [[0 for j in range(n)] for i in range(m)]
        paths[0][0] = 1
        for i in range(m):
            for j in range(n):
                tmp = 0
                if i==0 and j==0:
                    tmp += 1
                if i>0:
                    tmp += paths[i-1][j]
                if j>0:
                    tmp += paths[i][j-1]
                paths[i][j] = tmp
        return paths[m-1][n-1]

12.8

巧了嘛这不是，昨天刚好在复习回溯法解N皇后

题目

842. 将数组拆分成斐波那契序列

难度中等

给定一个数字字符串 S，比如 S = "123456579"，我们可以将它分成斐波那契式的序列 [123, 456, 579]。

形式上，斐波那契式序列是一个非负整数列表 F，且满足：

• 0 <= F[i] <= 2^31 - 1，（也就是说，每个整数都符合 32 位有符号整数类型）；
• F.length >= 3；
• 对于所有的0 <= i < F.length - 2，都有 F[i] + F[i+1] = F[i+2] 成立。

另外，请注意，将字符串拆分成小块时，每个块的数字一定不要以零开头，除非这个块是数字 0 本身。

返回从 S 拆分出来的任意一组斐波那契式的序列块，如果不能拆分则返回 []。

示例 1：

输入："123456579"
输出：[123,456,579]

示例 2：

输入: "11235813"
输出: [1,1,2,3,5,8,13]

示例 3：

输入: "112358130"
输出: []
解释: 这项任务无法完成。

示例 4：

输入："0123"
输出：[]
解释：每个块的数字不能以零开头，因此 "01"，"2"，"3" 不是有效答案。

示例 5：

输入: "1101111"
输出: [110, 1, 111]
解释: 输出 [11,0,11,11] 也同样被接受。

提示：

1. 1 <= S.length <= 200
2. 字符串 S 中只含有数字。

思路

就是常规的深搜+剪枝

• result用来存放可能的序列

• nums数组中存放已经存入当前序列的数字

• index用来标记当前应该从S的哪个位置开始遍历

• 递归函数dfs

  • 结束条件
    • 当前的index已经为S的长度时，说明我们已经遍历完整个字符串了
    • 如果当前的nums的长度≥3，说明这个序列是合理的，放到result中
    • 无论合理不合理，最后都需要退出递归
  • 可能路径
    • 如果当前nums的长度小于2，则从index开始，后面能组成的数字都是合理的，都可以加入路径继续搜索
    • 如果nums的长度≥2，则需要保证后面的数字是等于nums数组中最后两个数字之和，才可以加入路径继续搜索
  • 剪枝
    • 按照题目说明，如果我现在组成的数字是0开头，且长度大于1，就直接退出递归
    • 同理，如果当前尝试组成的数字大于2^31-1，也要退出递归
    • 同时，如果我当前组成的数字，已经超过了nums数组中最后两个数字之和，也是退出递归

代码

class Solution:
    def splitIntoFibonacci(self, S: str) -> List[int]:
        res = []
        def dfs(nums, index):
            if index == len(S) and len(nums)>=3:
                res.append(nums)
                return
            elif index>= len(S):
                return
            if len(nums)<2:
                for i in range(index+1, len(S)+1):
                    cur_num = int(S[index:i])
                    if i>index+1 and S[index]=='0' or cur_num>2147483647:
                        return
                    dfs(nums+[cur_num], i)
            else:
                target = nums[-1]+nums[-2]
                if target>2147483647:
                    return
                for i in range(index+1, len(S)+1):
                    cur_num = int(S[index:i])
                    if (i>index+1 and S[index]=='0'):
                        return
                    if cur_num<target:
                        continue
                    elif cur_num == target:
                        dfs(nums+[cur_num], i)
                    else:
                        return
        dfs([], 0)
        return res[0] if res else []
        

12.7

861. 翻转矩阵后的得分

难度中等

有一个二维矩阵 A 其中每个元素的值为 0 或 1 。

移动是指选择任一行或列，并转换该行或列中的每一个值：将所有 0 都更改为 1，将所有 1 都更改为 0。

在做出任意次数的移动后，将该矩阵的每一行都按照二进制数来解释，矩阵的得分就是这些数字的总和。

返回尽可能高的分数。

示例：

输入：[[0,0,1,1],[1,0,1,0],[1,1,0,0]]
输出：39
解释：
转换为 [[1,1,1,1],[1,0,0,1],[1,1,1,1]]
0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39

提示：

1. 1 <= A.length <= 20
2. 1 <= A[0].length <= 20
3. A[i][j] 是 0 或 1

思路

贪心法

• 首先通过行的移动保证每行第一个元素为1
• 然后对第一列以后的所有列进行移动
  • 保证每列的1比0多

代码

class Solution:
    def matrixScore(self, A: List[List[int]]) -> int:
        # 先通过行变化把第一列全部变成1
        rows, cols = len(A), len(A[0])
        for i in range(rows):
            if A[i][0] == 0:
                for j in range(cols):
                    A[i][j] = 1-A[i][j]
        
        # 再进行列变化使后面的列的1的个数尽可能多
        for j in range(1,cols):
            cnt_one, cnt_zero = 0, 0
            for i in range(rows):
                if A[i][j] == 1: cnt_one += 1
                else: cnt_zero += 1
            if cnt_zero>cnt_one:
                for i in range(rows):
                    A[i][j] = 1-A[i][j]
        # 求和
        res = 0
        for row in A:
            tmp = 0
            for j in range(cols):
                tmp += row[j]*2**(cols-j-1)
            res += tmp
        return res

12.6

好久没做简单题了👶

题目

118. 杨辉三角

难度简单

给定一个非负整数 *numRows，*生成杨辉三角的前 numRows 行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

思路

• 没啥思路，模拟就完事儿了

  因为不小心把两层循环都写成了i，调试了半天😓

代码

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        res = []
        last_row= []
        for i in range(numRows):
            cur_row = [1]
            for j in range(0,len(last_row)-1):
                cur_row.append(last_row[j]+last_row[j+1])
            if i>0:
                cur_row.append(1)
            res.append(cur_row)
            last_row = cur_row
        return res

12.5

题目

621. 任务调度器

难度中等

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

示例 1：

输入：tasks = ["A","A","A","B","B","B"], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
     在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。 

示例 2：

输入：tasks = ["A","A","A","B","B","B"], n = 0
输出：6
解释：在这种情况下，任何大小为 6 的排列都可以满足要求，因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类

示例 3：

输入：tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出：16
解释：一种可能的解决方案是：
     A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A

提示：

• 1 <= task.length <= 104
• tasks[i] 是大写英文字母
• n 的取值范围为 [0, 100]

思路

自己写了个模拟的方法，时间复杂度O(nlogn)，结果超过8%😓

标准数学解法的时间复杂度是O(N)

• 我们把时间分成一块儿一块儿的，每一块为n+1
  • 完成任务相当于往每个时间快内加入一个任务
  • 这样做的话，最后一个时间块内(最后一个时间块长度<=n+1)，我们必定需要完成那个次数最多的任务
    • 比如我总共需要做3次A，2次B，1次C，n设为3，那么我最后一个时间块内必定要完成A任务，且只需要完成A任务即可结束
  • 所以，我们只要求出某个任务出现的最大次数，就能知道我们要分多少个块
  • 求出块数之后，只要确定最后一个时间块的大小，即可确定完成所有任务所需时间
• 最后一个时间块的大小 = 出现次数为最大次数的任务个数
  • 比如3次A，2次B，1次C，那么最后一个时间块只需要完成一个A
  • 3次A，10次B，10次C，那么最后一个时间块内就需要完成B和C
• 因此，我们只需要确定任务出现的最大次数，以及最大次数的任务个数，即可直接求出所需要总时间

代码

class Solution:
    def leastInterval(self, tasks: List[str], n: int) -> int:
        dic = collections.defaultdict(int)
        for i in tasks:
            dic[i] += 1
        # 任务的最大次数
        max_cnt = max(dic.values())
        # 最大次数任务的个数
        max_job = len([i for i in dic if dic[i]==max_cnt])
        return max((n+1)*(max_cnt-1)+max_job, len(tasks))

12.4

题目

659. 分割数组为连续子序列

难度中等

给你一个按升序排序的整数数组 num（可能包含重复数字），请你将它们分割成一个或多个子序列，其中每个子序列都由连续整数组成且长度至少为 3 。

如果可以完成上述分割，则返回 true ；否则，返回 false 。

示例 1：

输入: [1,2,3,3,4,5]
输出: True
解释:
你可以分割出这样两个连续子序列 : 
1, 2, 3
3, 4, 5

示例 2：

输入: [1,2,3,3,4,4,5,5]
输出: True
解释:
你可以分割出这样两个连续子序列 : 
1, 2, 3, 4, 5
3, 4, 5

示例 3：

输入: [1,2,3,4,4,5]
输出: False

提示：

1. 输入的数组长度范围为 [1, 10000]

思路

• 贪心法
  • 构建两个字典
    • 一个计数字典nc
    • 一个子序列字典tail
      • tail[num]=i表示有i个以num为结尾的子序列
  • 遍历nums
    • 设当前遍历的数为num
    • 如果当前这个数字已经被用掉了，即nc[num]==0，直接跳过
    • 否则，查看一下有没有以num-1为结尾的子序列，即tail[num-1]>0
      • 如果有，则增加一条以num为结尾的子序列，同时要去掉一条以num-1为结尾的子序列
    • 如果没有，就尝试构建一条新的子序列，以num为首部，跟上num+1和num+2，用掉对应的数字，然后增加一条以num+2为结尾的子序列
    • 如果无法延长已有子序列也无法构建新序列，就返回False
  • 成功遍历完，就返回True

代码

from collections import defaultdict
class Solution:
    def isPossible(self, nums: List[int]) -> bool:
        nc, tail = defaultdict(int), defaultdict(int)
        for num in nums:
            nc[num] += 1
        for num in nums:
            if nc[num] == 0:
                continue
            elif tail[num-1]:
                nc[num] -= 1
                tail[num-1] -=1
                tail[num] += 1
            elif not tail[num-1]:
                if nc[num] and nc[num+1] and nc[num+2]:
                    tail[num+2] += 1
                    nc[num] -= 1
                    nc[num+1] -=1
                    nc[num+2] -=1
                else:
                    return False
            else:
                return False
        return True
        

12.3

204. 计数质数

难度简单

统计所有小于非负整数 n 的质数的数量。

示例 1：

输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：0

提示：

• 0 <= n <= 5 * 106

思路

• 假设2为质数，那么2的倍数就都不是质数
• 假设3为质数，那么3的倍数就都不是质数
• 低效率的实现方法（我一开始写的）
  • 新建一个集合nums，把[2,n-1]中的全部数字放进去
  • 然后遍历[2,n-1]
    • 如果当前遍历的数字x还在nums中，就把x的倍数全部删掉
    • 同时统计删除的个数
  • 计算总共删掉的个数和总的数字个数，得出素数个数
• 改进后的方法
  • 新建一个数组nums，长度为n，初始化所有元素为1
  • 遍历[2,n-1]
    • 如果nums[x]==1，说明这个数字为质数，计数器+1
    • 因为这个数字是质数，所以对它的倍数进行删除操作，全部置为0
  • 最后返回计数器

一开始我以为是集合导致的速度慢，但是我把方法1改成了数组实现还是很慢

应该是进行了太多次加减计算？

代码

• 方法1

class Solution:
    def countPrimes(self, n: int) -> int:
        if n<=1:
            return 0
        nums = set()
        for i in range(2,n):
            nums.add(i)
        
        def del_num(nums, num):
            cnt = 0
            if num not in nums: return 0
            for i in range(2*num,n+1,num):
                if i in nums:
                    nums.remove(i)
                    cnt += 1
            return cnt
        res = n-2
        for i in range(2,n):
            res -= del_num(nums, i)
        return res

• 方法2

class Solution:
    def countPrimes(self, n: int) -> int:
        nums = [1 for i in range(n)]
        cnt = 0
        for i in range(2,n):
            if nums[i]:
                cnt += 1
                for j in range(2*i,n,i):
                    nums[j] = 0
        return cnt

12.2

手动裂开（自行脑补微信新表情）

题目

321. 拼接最大数

难度困难

给定长度分别为 m 和 n 的两个数组，其元素由 0-9 构成，表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数，要求从同一个数组中取出的数字保持其在原数组中的相对顺序。

求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。

说明: 请尽可能地优化你算法的时间和空间复杂度。

示例 1:

输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]

示例 2:

输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:
[6, 7, 6, 0, 4]

示例 3:

输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:
[9, 8, 9]

思路

是真的看不出来该怎么做

根据题解写个大概思路

• 参考了官方题解和这个兄弟的题解

• 要从两个数组中挑选k个数字出来，拼成最大序列，总体来说需要两步

  1. 从第一个数组中挑选i个数字组成最大子序列seq1，从第二个数组中挑选k-i个数字组成最大子序列seq2
  2. 根据某种规则，把这两个最大子序列合并成一个最大子序列

• ✨从数组nums中，找出长度为size的最大子序列方法

  • 新建一个空栈stk
  • 设定一个最大抛弃值drop
    • drop=数组的长度-size
  • 遍历nums中的数字
    • 如果栈非空，且当前遍历的数字比栈顶元素大
      • 就一直抛弃栈顶元素，每次抛弃一个元素，drop -= 1
      • 直到栈空或者drop=0
    • 把当前遍历的这个数字放到栈里
  • 返回栈的前size个数字，就是最大子序列

• ✨把两个最大子序列seq1和seq2合并成一个最大子序列的方法

  • 不断从seq1或者seq2中取首部的数字

    • 每次从字典序大的那个子序列中取数字

    • python中两个数组直接对比，获得是按字典序比较的结果

      比如[2,7,1,4]>[2,3,3,6]，因为这里的第0位相等，第1位上3>1

    • 这么做的原因是能保证每次取完数字之后，下一次比较的时候能取到尽可能大的数

      如果我先从[2,3,3,6]中取了首数字，第二步就变成了从[3,3,6]和[2,7,1,4]中取数字

      这样合并出来的子序列就从2->7变成了2->3，那就不是最大子序列了

  • 每次取完首部数字之后，记得要把这个数字给移除

小生愚钝，不吝赐教，欢迎指教

代码

class Solution:
    def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:
        # 找到最大子序列的方法
        def get_max_sequence(nums, size):
            # 从nums数组中，找到长度为size的最大子序列
            # 利用栈
            stk = []
            # drop是用来保证最后的子序列长度不小于size
            drop = len(nums)-size
            for num in nums:
                while drop and stk and stk[-1]<num:
                    stk.pop()
                    drop -=1
                stk.append(num)
            return stk[:size]

        def merge(seq1, seq2):
            # 把两个最大子序列合并成一个最大子序列
            res = []
            while seq1 or seq2:
                # 每次加入一个较大子序列的首位数
                tmp = seq1 if seq1>seq2 else seq2
                res.append(tmp[0])
                # 插入一个数字之后要删掉原序列中的数字
                tmp.pop(0)
            return res
        
        # 循环两个子序列的可能长度
        res = [0 for i in range(k)]
        for i in range(k+1):
            if i<=len(nums1) and k-i<=len(nums2):
                tmp = merge(get_max_sequence(nums1, i), get_max_sequence(nums2, k-i))
                res = max(res, tmp)
        return res

12.1

美好的一天从偷懒开始

题目

34. 在排序数组中查找元素的第一个和最后一个位置

难度中等691

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：

• 你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109
• nums 是一个非递减数组
• -109 <= target <= 109

思路

• 面试官觉得很无聊的两个思路
  1. 从头开始遍历，从尾部开始遍历，找到数字出现的两个位置
  2. 用python封装好的方法，先正序用index方法找到target的第一次出现位置，再把数组逆序一下找到target的第一次出现位置

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if target not in nums:
            return [-1, -1]
        else:
            return [nums.index(target), len(nums)-1-nums[::-1].index(target)]

• 但止步于这两个无脑方法肯定是不行的

• 看进阶的时间复杂度要求 O(log n)就知道肯定是二分，相当于把python封装的方法自己实现一遍

  自己写一个二分能因为细节提交错好多次

代码

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if not len(nums):
            return [-1,-1]
        left, right = 0, len(nums)-1
        index = -1
        while left<=right:
            mid = (left+right+1)//2
            if nums[mid]==target:
                index = mid
                break
            if nums[mid]>target:
                right = mid-1
            else:
                left = mid+1
        if index==-1:
            return [-1,-1]
        start, end = index, index
        while start>=0 and nums[start]==target:
            start -= 1
        start += 1
        while end<len(nums) and nums[end]==target:
            end+=1
        end-=1
        return [start, end]