2021年5月刷题日志
5.31
这么快就五月最后一天啦。
题目
342. 4的幂
难度简单
给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回
true;否则,返回false。
思路
没高兴动脑子,就和昨天一样的解法。
代码
class Solution:
def isPowerOfFour(self, n: int) -> bool:
while n > 1:
if n % 4 != 0:
return False
n //= 4
return n == 1
5.30
题目
231. 2 的幂
难度简单
给你一个整数
n,请你判断该整数是否是 2 的幂次方。如果是,返回true;否则,返回false。如果存在一个整数
x使得n == 2x,则认为n是 2 的幂次方。示例 1:
输入:n = 1 输出:true 解释:20 = 1示例 2:
输入:n = 16 输出:true 解释:24 = 16示例 3:
输入:n = 3 输出:false示例 4:
输入:n = 4 输出:true示例 5:
输入:n = 5 输出:false提示:
-2^31 <= n <= 2^31 - 1
思路
- 循环
log函数
代码
# 循环
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
while n > 1:
if n % 2 == 1: return False
n //= 2
return n == 1
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return n > 0 and 2 ** int(math.log(n, 2)) == n
5.29
题目
1074. 元素和为目标值的子矩阵数量
难度困难
给出矩阵
matrix和目标值target,返回元素总和等于目标值的非空子矩阵的数量。子矩阵
x1, y1, x2, y2是满足x1 <= x <= x2且y1 <= y <= y2的所有单元matrix[x][y]的集合。如果
(x1, y1, x2, y2)和(x1', y1', x2', y2')两个子矩阵中部分坐标不同(如:x1 != x1'),那么这两个子矩阵也不同。示例 1:
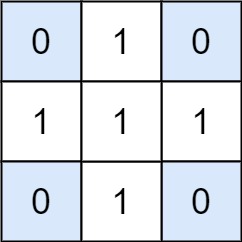
输入:matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0 输出:4 解释:四个只含 0 的 1x1 子矩阵。示例 2:
输入:matrix = [[1,-1],[-1,1]], target = 0 输出:5 解释:两个 1x2 子矩阵,加上两个 2x1 子矩阵,再加上一个 2x2 子矩阵。示例 3:
输入:matrix = [[904]], target = 0 输出:0*提示:*
1 <= matrix.length <= 1001 <= matrix[0].length <= 100-1000 <= matrix[i] <= 1000-10^8 <= target <= 10^8
思路
首先需要进行一波预处理,生成二维前缀和数组,用来快速计算子矩阵和。
然后从朴素的角度出发,需要枚举所有的子矩阵,但是这边可以使用一个巧妙的优化方法。
- 进行纵向扫描👇,枚举子矩阵可能的所有首行和末行的位置。
- 对于确定的首行和末行,新建一个哈希表用来记录子列和的出现次数,并且初始化
dic[0] = 1。- 进行横向的扫描👉,即每次计算某一列的和。
- 如果发现
当前的子列和 - target在哈希表中出现过,说明有子矩阵可以满足和为target,更新res。 - 根据当前的子列和更新哈希表。
代码
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
# 二维前缀和
m, n = len(matrix), len(matrix[0])
sums = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(m):
for j in range(n):
sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] + matrix[i][j] - sums[i][j]
res = 0
# 枚举子矩阵
for r1 in range(m + 1): # 枚举矩阵首行
for r2 in range(r1 + 1, m + 1): # 枚举矩阵末行
dic = defaultdict(int) # 用来记录子列和的出现次数
dic[0] = 1 # 初始化
for c in range(1, n + 1):
cur_sum = sums[r2][c] - sums[r1][c]
if cur_sum - target in dic:
res += dic[cur_sum - target]
dic[cur_sum] += 1
return res
5.28
收到 MS 的 onboard 通知啦,交完最后一份材料就等着过两周实习去咯。
题目
477. 汉明距离总和
难度中等
两个整数的 汉明距离 指的是这两个数字的二进制数对应位不同的数量。
计算一个数组中,任意两个数之间汉明距离的总和。
示例:
输入: 4, 14, 2 输出: 6 解释: 在二进制表示中,4表示为0100,14表示为1110,2表示为0010。(这样表示是为了体现后四位之间关系) 所以答案为: HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.注意:
- 数组中元素的范围为从
0到10^9。- 数组的长度不超过
10^4。
思路
呜呜呜,中等题我竟然也要看题解。
因为需要计算任意两个数的汉明距离的总和,所以本质上是一个全排列。
但是直接计算全排列中每一对数的异或后 1 的个数时间复杂度太高,因此可以巧妙地转换成按位来计算 1 的个数。
- 先遍历一遍数组,统计每个位置的
1的个数,比如1, 2, 5,就会统计得到dic[0] = 2, dic[1] = 1, dic[2] = 1。 - 因为是全排列,所以每个位置都会进行 $n \times n$ 次对比,其中 $n$ 表示数组长度。最后计算得到的汉明距离只包括
0 和 1对,因此就是 $n \times (n - cnt)$,其中cnt是该位置上1的出现次数。
代码
class Solution:
def totalHammingDistance(self, nums: List[int]) -> int:
# 统计每个位置的1的个数
dic = defaultdict(int)
for num in nums:
# 从第30位枚举到第1位
for k in range(29, -1, -1):
bit = (num >> k) & 1
if bit == 1:
dic[k] += 1
n = len(nums)
# 每个位置的和为 dic[i] * (n - dic[i])
res = 0
for i in range(30):
res += dic[i] * (n - dic[i])
return res
5.27
回归简单的快乐。
题目
461. 汉明距离
难度简单
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数
x和y,计算它们之间的汉明距离。示例:
输入: x = 1, y = 4 输出: 2 解释: 1 (0 0 0 1) 4 (0 1 0 0) ↑ ↑ 上面的箭头指出了对应二进制位不同的位置。
思路
统计 x 和 y 异或出来的结果的二进制 1 个数。
- 通过函数转换成二进制字符串之后统计
1的个数。 - 通过
&和<<每次计算结果的最后一位是否为1同时右移一位。
代码
# 1. 转换二进制字符串并计数
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
return bin(x ^ y).count('1')
# 2. 位运算计数
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
k = x ^ y
cnt = 0
while k:
cnt += k & 1
k >>= 1
return cnt
5.26
昨天极难直接跳过。
题目
1190. 反转每对括号间的子串
难度中等
给出一个字符串
s(仅含有小写英文字母和括号)。请你按照从括号内到外的顺序,逐层反转每对匹配括号中的字符串,并返回最终的结果。
注意,您的结果中 不应 包含任何括号。
示例 1:
输入:s = "(abcd)" 输出:"dcba"示例 2:
输入:s = "(u(love)i)" 输出:"iloveu"示例 3:
输入:s = "(ed(et(oc))el)" 输出:"leetcode"示例 4:
输入:s = "a(bcdefghijkl(mno)p)q" 输出:"apmnolkjihgfedcbq"提示:
0 <= s.length <= 2000s中只有小写英文字母和括号- 我们确保所有括号都是成对出现的
思路
用栈来模拟反转的过程,把字符逐个放入栈中,分两种情况处理:
- 当前字符为字母或
(,直接存入栈 - 当前字符为
),这个时候我们需要翻转的是直至上一个(为止的字符,通过在新建一个栈倒序放字符实现翻转即可。
代码
class Solution:
def reverseParentheses(self, s: str) -> str:
n = len(s)
# 栈模拟
stk = []
for i in s:
if i == ')':
# 找到左括号
t = []
while stk[-1] != '(':
t.append(stk.pop())
stk.pop()
stk += t
else:
stk.append(i)
return "".join(stk)
5.24
又是困难 🤦♂️
题目
664. 奇怪的打印机
难度困难
有台奇怪的打印机有以下两个特殊要求:
- 打印机每次只能打印由 同一个字符 组成的序列。
- 每次可以在任意起始和结束位置打印新字符,并且会覆盖掉原来已有的字符。
给你一个字符串
s,你的任务是计算这个打印机打印它需要的最少打印次数。示例 1:
输入:s = "aaabbb" 输出:2 解释:首先打印 "aaa" 然后打印 "bbb"。示例 2:
输入:s = "aba" 输出:2 解释:首先打印 "aaa" 然后在第二个位置打印 "b" 覆盖掉原来的字符 'a'。提示:
1 <= s.length <= 100s由小写英文字母组成
思路
动态规划,动态转移方程的前提是要知道,如果字符串中的一个子串的头尾字母相同,那么在打印首字母的同时就可以打印尾字母。
由于我对区间DP的理解比较浅,解释不清,建议直接看题解
代码
class Solution:
def strangePrinter(self, s: str) -> int:
n = len(s)
# dp[i][j] 表示从i到j的最少打印次数
dp = [[0] * n for _ in range(n + 1)]
for l in range(n): # 区间长度
for i in range(n - l): # 区间起点
j = i + l # 区间结尾
dp[i][j] = dp[i + 1][j] + 1 # 默认变首字母,需要+1
for k in range(i + 1, j + 1): # 分割点
if s[k] == s[i]:
dp[i][j] = min(dp[i][j], dp[i][k - 1] + dp[k + 1][j])
return dp[0][n - 1]
5.23
谁能想到昨天写了题解却没提交呢 😰 不过昨天答辩拿了省二还不错。
题目
1707. 与数组中元素的最大异或值
难度困难
给你一个由非负整数组成的数组
nums。另有一个查询数组queries,其中queries[i] = [xi, mi]。第
i个查询的答案是xi和任何nums数组中不超过mi的元素按位异或(XOR)得到的最大值。换句话说,答案是max(nums[j] XOR xi),其中所有j均满足nums[j] <= mi。如果nums中的所有元素都大于mi,最终答案就是-1。返回一个整数数组
answer作为查询的答案,其中answer.length == queries.length且answer[i]是第i个查询的答案。示例 1:
输入:nums = [0,1,2,3,4], queries = [[3,1],[1,3],[5,6]] 输出:[3,3,7] 解释: 1) 0 和 1 是仅有的两个不超过 1 的整数。0 XOR 3 = 3 而 1 XOR 3 = 2 。二者中的更大值是 3 。 2) 1 XOR 2 = 3. 3) 5 XOR 2 = 7.示例 2:
输入:nums = [5,2,4,6,6,3], queries = [[12,4],[8,1],[6,3]] 输出:[15,-1,5]
思路
周末两道异或困难题,真狠呐。
不过这道题的思路是和一周前那道差不多,都是通过构造字典树,贪心法求最大值。
我们根据 queries 中的 m 的从小到大的顺序,逐个求最大异或值,这样能够保证每次字典树上的所有分支组成的值比 m 小。
贪心的思路则是,从 x 的最高位开始,字典树上的结点能取反则取反,保证异或的结果尽可能高的位是 1 。
唯一要注意的是,在对 queries 排序的时候,需要保存每个 query 原来的位置,在输出答案的时候需要用到。
代码
class Trie:
def __init__(self):
# left: 0, right: 1
self.left = None
self.right = None
class Solution:
def maximizeXor(self, nums: List[int], queries: List[List[int]]) -> List[int]:
root = Trie()
nums.sort(reverse = True)
newQueries = sorted(enumerate(queries),key=lambda x:x[1][1])
def build(val):
node = root
for k in range(30, -1, -1):
bit = (val >> k) & 1
if bit == 0:
if not node.left:
node.left = Trie()
node = node.left
else:
if not node.right:
node.right = Trie()
node = node.right
return
res = [0] * len(queries)
for idx, [x, m] in newQueries:
while nums and nums[-1] <= m:
build(nums.pop())
maxRes = 0
node = root
for k in range(30, -1, -1):
if not node:
res[idx] = -1
break
bit = (x >> k) & 1
mBit = (m >> k) & 1
if bit == 0:
if node.right:
node = node.right
maxRes = maxRes * 2 + 1
else:
node = node.left
maxRes *= 2
else:
if node.left:
node = node.left
maxRes = maxRes * 2 + 1
else:
node = node.right
maxRes *= 2
else:
res[idx] = maxRes
return res
5.22
镇江比赛现场,答辩前刷道每日一题。
题目
810. 黑板异或游戏
难度困难
黑板上写着一个非负整数数组
nums[i]。Alice 和 Bob 轮流从黑板上擦掉一个数字,Alice 先手。如果擦除一个数字后,剩余的所有数字按位异或运算得出的结果等于 0 的话,当前玩家游戏失败。 (另外,如果只剩一个数字,按位异或运算得到它本身;如果无数字剩余,按位异或运算结果为 0。)换种说法就是,轮到某个玩家时,如果当前黑板上所有数字按位异或运算结果等于 0,这个玩家获胜。
假设两个玩家每步都使用最优解,当且仅当 Alice 获胜时返回
true。示例:
输入: nums = [1, 1, 2] 输出: false 解释: Alice 有两个选择: 擦掉数字 1 或 2。 如果擦掉 1, 数组变成 [1, 2]。剩余数字按位异或得到 1 XOR 2 = 3。那么 Bob 可以擦掉任意数字,因为 Alice 会成为擦掉最后一个数字的人,她总是会输。 如果 Alice 擦掉 2,那么数组变成[1, 1]。剩余数字按位异或得到 1 XOR 1 = 0。Alice 仍然会输掉游戏。提示:
1 <= N <= 10000 <= nums[i] <= 2^16
思路
博弈论,详细数学证明过程可以看官方题解。
Alice 有两种必胜情况:
- 数组中所有数异或的结果是 0(不管是什么顺序, 必然是先手的将数组清空)
- 数组的长度为偶数(可以通过数学证明先手必定能异或到最后一个数)
代码
class Solution:
def xorGame(self, nums: List[int]) -> bool:
res = 0
for num in nums:
res ^= num
return res == 0 or nums.length % 2 == 0
5.21
题目
1035. 不相交的线
难度中等
在两条独立的水平线上按给定的顺序写下
nums1和nums2中的整数。现在,可以绘制一些连接两个数字
nums1[i]和nums2[j]的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
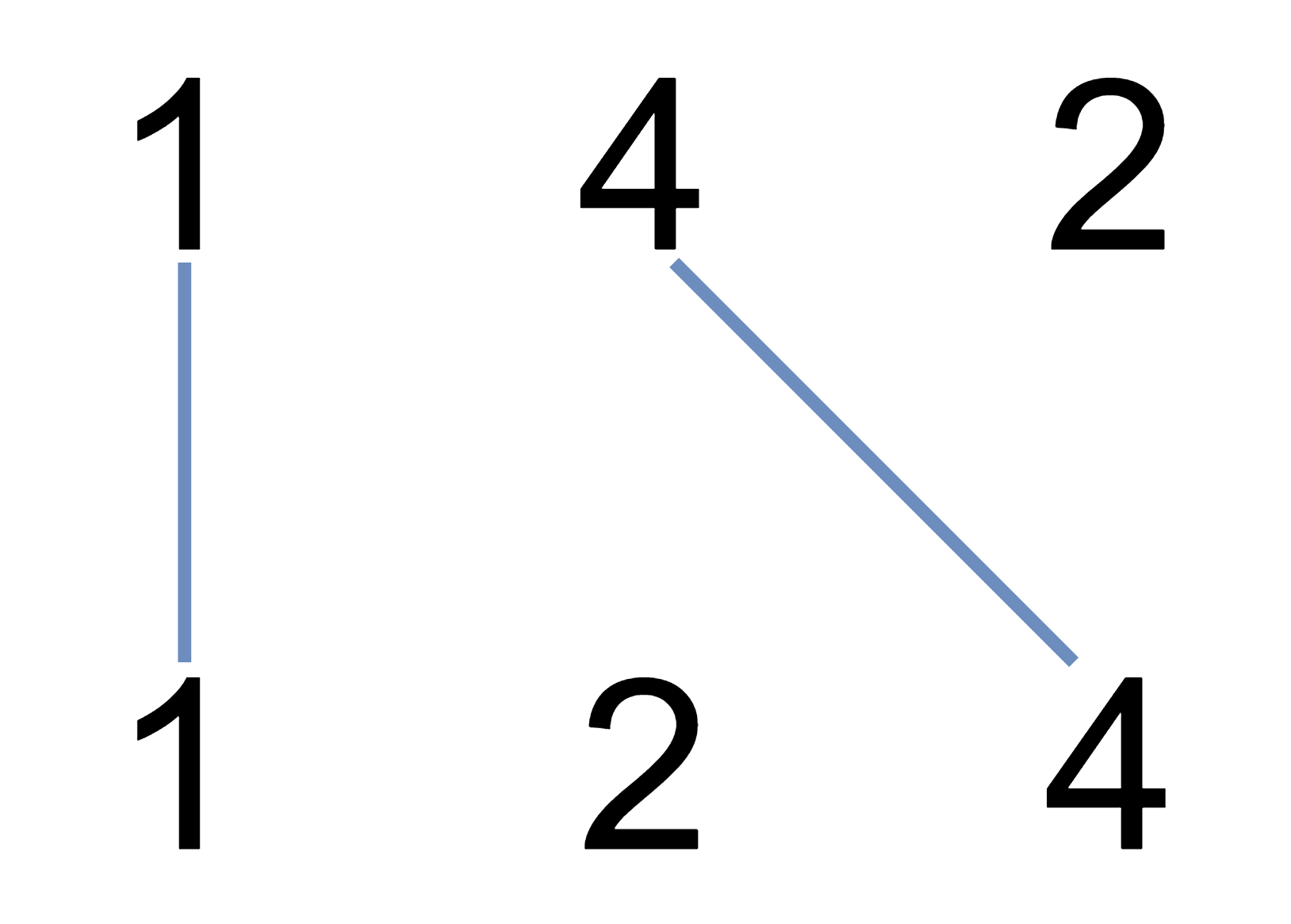
输入:nums1 = [1,4,2], nums2 = [1,2,4] 输出:2 解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] 输出:3示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] 输出:2提示:
1 <= nums1.length <= 5001 <= nums2.length <= 5001 <= nums1[i], nums2[i] <= 2000
思路
第一直觉是 DFS,结果十分钟写完之后超时了 💫
看了题解发现是动规,思想就是最长公共子序列,写呗。
代码
昨天还忘记说了用 Python 的原因,是六月份有个蓝桥杯国赛。
class Solution:
def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
m, n = len(nums1), len(nums2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if nums1[i - 1] == nums2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[m][n]
5.20
昨晚得知了 MS 实习被分到 NLP 组的消息 🤦♂️ 吓得我以为前端的梦破灭了,后来询问学长发现其实还是做全栈偏前端的项目。
题目
692. 前K个高频单词
难度中等
给一非空的单词列表,返回前 k 个出现次数最多的单词。
返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率,按字母顺序排序。
示例 1:
输入: ["i", "love", "leetcode", "i", "love", "coding"], k = 2 输出: ["i", "love"] 解析: "i" 和 "love" 为出现次数最多的两个单词,均为2次。 注意,按字母顺序 "i" 在 "love" 之前。示例 2:
输入: ["the", "day", "is", "sunny", "the", "the", "the", "sunny", "is", "is"], k = 4 输出: ["the", "is", "sunny", "day"] 解析: "the", "is", "sunny" 和 "day" 是出现次数最多的四个单词, 出现次数依次为 4, 3, 2 和 1 次。
思路
哈希表计数 + 排序
代码
class Solution:
def topKFrequent(self, words: List[str], k: int) -> List[str]:
dic = defaultdict(int)
for word in words:
dic[word] += 1
res = list(dic.items())
res.sort(key = lambda x: (-x[1], x[0]))
return [i[0] for i in res[:k]]
5.19
题目
1738. 找出第 K 大的异或坐标值
难度中等
给你一个二维矩阵
matrix和一个整数k,矩阵大小为m x n由非负整数组成。矩阵中坐标
(a, b)的 值 可由对所有满足0 <= i <= a < m且0 <= j <= b < n的元素matrix[i][j](下标从 0 开始计数)执行异或运算得到。请你找出
matrix的所有坐标中第k大的值(k的值从 1 开始计数)。示例 1:
输入:matrix = [[5,2],[1,6]], k = 1 输出:7 解释:坐标 (0,1) 的值是 5 XOR 2 = 7 ,为最大的值。示例 2:
输入:matrix = [[5,2],[1,6]], k = 2 输出:5 解释:坐标 (0,0) 的值是 5 = 5 ,为第 2 大的值。
思路
似曾相识,不久之前做过一次二维前缀和,一个性质。
开辟一个二维数组 sums 计算从左上角开始的累计异或值,sums[i][j] 表示的是从 matrix[0][0] 一直异或到 matrix[i - 1][j - 1] 的值。
通过遍历一遍 martix 来生成该二维数组,要计算 sums[i][j] 只需要将对以下四个值进行异或操作。
-
sums[i - 1][j - 1] -
sums[i - 1][j] -
sums[i][j - 1] -
matrix[i][j]
代码
function kthLargestValue(matrix: number[][], k: number): number {
// 类前缀和,二维异或版
let m = matrix.length, n = matrix[0].length
const sum = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0))
const nums = []
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
sum[i + 1][j + 1] = sum[i][j] ^ sum[i + 1][j] ^ sum[i][j + 1] ^ matrix[i][j]
nums.push(sum[i + 1][j + 1])
}
}
nums.sort((x, y) => y - x)
return nums[k-1]
};
5.18
题目
1442. 形成两个异或相等数组的三元组数目
难度中等
给你一个整数数组
arr。现需要从数组中取三个下标
i、j和k,其中(0 <= i < j <= k < arr.length)。
a和b定义如下:
a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]注意:^ 表示 按位异或 操作。
请返回能够令
a == b成立的三元组 (i,j,k) 的数目。示例 1:
输入:arr = [2,3,1,6,7] 输出:4 解释:满足题意的三元组分别是 (0,1,2), (0,2,2), (2,3,4) 以及 (2,4,4)示例 2:
输入:arr = [1,1,1,1,1] 输出:10
思路
还算是看完题解就能立马就能看懂的题。
为了快速获取 arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1] 这种连续异或值,首先需要考虑使用类前缀和数组。
表面上看需要三重循环穷举 i, j ,k 的值,但是这里有一个小 trick,当我找到一对 i, j, k 满足题目要求时,事实上这个 j 的位置并不重要,或者说它在哪都都无所谓。
因为如果 j 前移,根据异或的性质,新的 a, b 可以根据 a ^ arr[j - 1], b ^ arr[j - 1] 求出,显然此时 a, b 还是相等。
所以只需要穷举 i ,k 的值即可知道所有的可能性。
代码
function countTriplets(arr: number[]): number {
// arr[i:j], arr[j+1:k+1]
// 类前缀和
const n = arr.length
const sum = new Array(n + 1)
for (let i = 0; i < n; i++) {
// arr[i:j] = sum[j] ^ sum[i]
sum[i + 1] = sum[i] ^ arr[i]
}
// a ^ b = (a ^ x) ^ (b ^ x)
// a中少一个,b中多一个,结果不变,只需要循环i, k
let res = 0
for (let i = 0; i < n - 1; i++) {
for (let k = i + 1; k < n; k++) {
if ((sum[i] ^ sum[k]) === arr[k]) res += (k - i)
}
}
return res
};
5.17
题目
993. 二叉树的堂兄弟节点
难度简单
在二叉树中,根节点位于深度
0处,每个深度为k的节点的子节点位于深度k+1处。如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点
root,以及树中两个不同节点的值x和y。只有与值
x和y对应的节点是堂兄弟节点时,才返回true。否则,返回false。示例 1:
输入:root = [1,2,3,4], x = 4, y = 3 输出:false示例 2:
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4 输出:true
思路
简单题,既然之前一直 DFS,这次就换个 BFS 吧。
利用数组进行层序的遍历,每次遍历做的事情:
- 检查上一层的结点值,如果同时发现
x和y,返回true,如果只有其中之一,返回false,两者都没出现,继续找。 - 存储下一层的结点值
- 判断当前的结点的两个子节点是否正好是
x和y,如果是,说明两者是亲兄弟关系,和题目不符,返回false。
代码
function isCousins(root: TreeNode | null, x: number, y: number): boolean {
// 层序遍历
let nodes = [root]
while (nodes.length) {
const nxt = []
let existsX = false, existsY = false
for (let node of nodes) {
if (node.val === x) existsX = true
if (node.val === y) existsY = true
if (node.left) {
nxt.push(node.left)
}
if (node.right) {
nxt.push(node.right)
}
if (node.left && node.right) {
if (node.left.val === x && node.right.val === y) return false
else if (node.left.val === y && node.right.val === x) return false
}
}
if (existsX && existsY) return true
else if (existsX || existsY) return false
nodes = nxt
}
return false
};
5.16
题目
421. 数组中两个数的最大异或值
难度中等
给你一个整数数组
nums,返回nums[i] XOR nums[j]的最大运算结果,其中0 ≤ i ≤ j < n。**进阶:**你可以在
O(n)的时间解决这个问题吗?示例 1:
输入:nums = [3,10,5,25,2,8] 输出:28 解释:最大运算结果是 5 XOR 25 = 28.示例 2:
输入:nums = [0] 输出:0示例 3:
输入:nums = [2,4] 输出:6示例 4:
输入:nums = [8,10,2] 输出:10示例 5:
输入:nums = [14,70,53,83,49,91,36,80,92,51,66,70] 输出:127
思路
官方给出了两种方法,一种是用哈希表,另一种是前缀树,这两种算法的核心思想是相同的:
- 要想知道数组中最大的两个数的异或值,我们就需要知道最大值的每个「位」是 1 还是 0。
- 假设我们已经知道了最大值前
i位,想要知道i + 1位的值,那为了令这个数尽可能大,则需要「贪心」地去令这个位为 1。 - 想要让这个位为 1 的方法也很朴素,在满足前
i位最大的数中,找到能使第i + 1位为 1 的数即可。
接下来解释一下怎么使用前缀树判断。
在本题中,由于每一位只可能是 1 或者 0,所以我们使用 left 指针表示 0,用 right 指针表示 1。
我们遍历数组进行建树,从每个数字的 31 位开始(不足补0),如果是 1,那么根节点就应该有右节点,反之,根节点就应该有左节点。详细过程见代码。
然后对我们枚举数组中每个数,逐个寻找异或最大值。
因为我们的树就是类似如下的,所以我们可以很快知道每个位置能不能取1。
代码
剪枝操作:遍历的同时判断最大异或值
interface Trie {
left?: Trie
right?: Trie
}
class Trie {
constructor() {
// left 代表 0,right 代表 1
this.left = null
this.right = null
}
}
function findMaximumXOR(nums: number[]): number {
const root = new Trie()
let res = 0
// 建立字典树
for (let i = 0; i < nums.length; i++) {
let node = root
for (let k = 30; k >= 0; k--){
let bit = (nums[i] >> k) & 1 // 左移 k 位
if (bit == 0) {
if (!node.left) {
node.left = new Trie()
}
node = node.left
} else if (bit == 1) {
if (!node.right) {
node.right = new Trie()
}
node = node.right
}
}
// 每次加入一个数字后 check 一下最大值
check(nums[i])
}
function check (num: number){
// 遍历字典树求最大可能的值
let node = root
let tmp = 0
for (let k = 30; k >= 0; k--) {
let bit = (num >> k) & 1
if (bit == 0) {
if (node.right) {
node = node.right
tmp = tmp * 2 + 1
} else {
node = node.left
tmp = tmp * 2
}
} else if (bit == 1) {
if (node.left) {
node = node.left
tmp = tmp * 2 + 1
} else {
node = node.right
tmp = tmp * 2
}
}
res = Math.max(tmp, res)
}
}
return res
};
5.15
昨天中等版,今天简单版,反着来?
题目
13. 罗马数字转整数
难度简单
罗马数字包含以下七种字符:
I,V,X,L,C,D和M。字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000例如, 罗马数字 2 写做
II,即为两个并列的 1。12 写做XII,即为X+II。 27 写做XXVII, 即为XX+V+II。通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做
IIII,而是IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:
输入: "III" 输出: 3示例 2:
输入: "IV" 输出: 4示例 3:
输入: "IX" 输出: 9示例 4:
输入: "LVIII" 输出: 58 解释: L = 50, V= 5, III = 3.示例 5:
输入: "MCMXCIV" 输出: 1994 解释: M = 1000, CM = 900, XC = 90, IV = 4.
思路
用哈希表存储每个字母代表的数字,顺序遍历一遍字符串,逐个转换。
每次除了把当前字母转换为数字,还要考虑以下前一个数字是否比当前数字小。
如果前小,需要扣掉两倍小数,例如 IX = 1 + 10 - 1 * 2 。
代码
function romanToInt(s: string): number {
const n = s.length
let res = 0
const map = new Map([['I', 1], ['V', 5], ['X', 10], ['L', 50], ['C', 100], ['D', 500], ['M', 1000]])
for (let i = 0; i < n; i++) {
res += map.get(s[i])
if (i > 0 && map.get(s[i-1]) < map.get(s[i])) {
res -= 2 * map.get(s[i-1])
}
}
return res
};
5.14
题目
12. 整数转罗马数字
难度中等
罗马数字包含以下七种字符:
I,V,X,L,C,D和M。字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000例如, 罗马数字 2 写做
II,即为两个并列的 1。12 写做XII,即为X+II。 27 写做XXVII, 即为XX+V+II。通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做
IIII,而是IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。给定一个整数,将其转为罗马数字。输入确保在 1 到 3999 的范围内。
示例 1:
输入: 3 输出: "III"示例 2:
输入: 4 输出: "IV"示例 3:
输入: 9 输出: "IX"示例 4:
输入: 58 输出: "LVIII" 解释: L = 50, V = 5, III = 3.示例 5:
输入: 1994 输出: "MCMXCIV" 解释: M = 1000, CM = 900, XC = 90, IV = 4.
思路
用简单题的解法做中等题,不过分吧 🙄
把数字和字母的对应关系存储到数组中,每次从大到小尝试减。
代码
function intToRoman(num: number): string {
const dic = [
[1000, 'M'],
[900, 'CM'],
[500, 'D'],
[400, 'CD'],
[100, 'C'],
[90, 'XC'],
[50, 'L'],
[40, 'XL'],
[10, 'X'],
[9, 'IX'],
[5, 'V'],
[4, 'IV'],
[1, 'I'],
]
let res = ""
while (num > 0) {
for (let [key, val] of dic) {
if (num >= key) {
num -= +key
res += val
break
}
}
}
return res
};
5.13
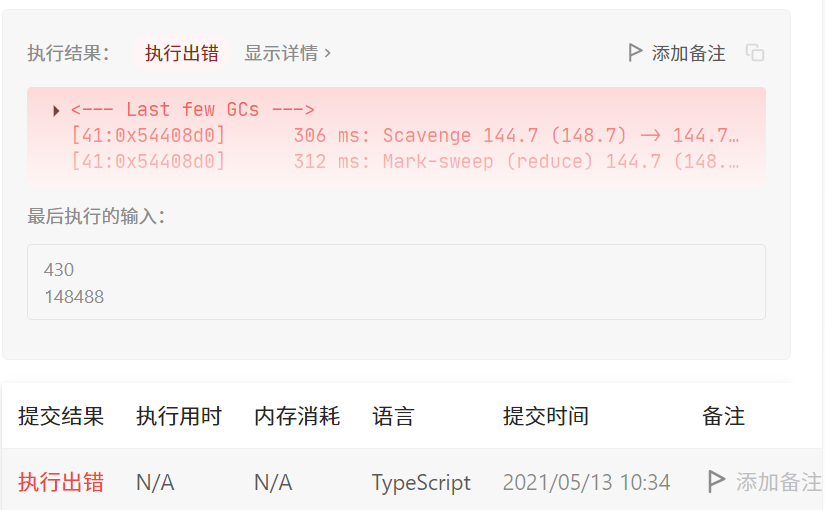
因为数组太大被迫优化空间,结果发现我耗时 3000ms,别人 100ms 😓。
题目
1269. 停在原地的方案数
难度困难
有一个长度为
arrLen的数组,开始有一个指针在索引0处。每一步操作中,你可以将指针向左或向右移动 1 步,或者停在原地(指针不能被移动到数组范围外)。
给你两个整数
steps和arrLen,请你计算并返回:在恰好执行steps次操作以后,指针仍然指向索引0处的方案数。由于答案可能会很大,请返回方案数 模
10^9 + 7后的结果。示例 1:
输入:steps = 3, arrLen = 2 输出:4 解释:3 步后,总共有 4 种不同的方法可以停在索引 0 处。 向右,向左,不动 不动,向右,向左 向右,不动,向左 不动,不动,不动示例 2:
输入:steps = 2, arrLen = 4 输出:2 解释:2 步后,总共有 2 种不同的方法可以停在索引 0 处。 向右,向左 不动,不动示例 3:
输入:steps = 4, arrLen = 2 输出:8提示:
1 <= steps <= 5001 <= arrLen <= 10^6
思路
虽然题目标了困难,但其实就是个经典动规。
DP table:本质上就是使用 dp[i][j] 来记录 第i步后,停留在第j格的方案数。
Base case:默认 dp[0][0] = 1,表示移动 0 步,停留在第 0 格的方案有一种。
动态转移方程:想知道 dp[i][j] ,只需要计算 dp[i-1][j-1] + dp[i-1][j] + dp[i-1][j+1],当然还需要保证位置合法。
最后答案就是 dp[steps][0] 啦。
代码在这个基础上进行了剪枝和空间优化。
代码
一开始我的数组
dp开辟的是arrLen大小的,因为我想着记录所有可能的位置。结果后来发现
steps最大只有 500 🤯,我佛啦,那arrLen最大10e6有个 🔨 用!
function numWays(steps: number, arrLen: number): number {
// 动规
// dp[i][j] 表示第 i 步后,停留在 j 格的方案数。
let dp = new Array(steps + 1).fill(0)
dp[0] = 1
for (let i = 1; i <= steps; i++) {
const newDp = new Array(steps + 1).fill(0)
for (let j = 0; j < Math.min(steps + 1, arrLen); j++) {
if (i == j) {
newDp[j] = 1
break
}
if (i < j) {
break
}
newDp[j] = dp[j]
if (j > 0) newDp[j] += dp[j - 1]
if (j < arrLen) newDp[j] += dp[j + 1]
newDp[j] %= 1000000007
}
dp = newDp
}
return dp[0]
};
5.12
题目
1310. 子数组异或查询
难度中等
有一个正整数数组
arr,现给你一个对应的查询数组queries,其中queries[i] = [Li, Ri]。对于每个查询
i,请你计算从Li到Ri的 XOR 值(即arr[Li] **xor** arr[Li+1] **xor** ... **xor** arr[Ri])作为本次查询的结果。并返回一个包含给定查询
queries所有结果的数组。示例 1:
输入:arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]] 输出:[2,7,14,8] 解释: 数组中元素的二进制表示形式是: 1 = 0001 3 = 0011 4 = 0100 8 = 1000 查询的 XOR 值为: [0,1] = 1 xor 3 = 2 [1,2] = 3 xor 4 = 7 [0,3] = 1 xor 3 xor 4 xor 8 = 14 [3,3] = 8示例 2:
输入:arr = [4,8,2,10], queries = [[2,3],[1,3],[0,0],[0,3]] 输出:[8,0,4,4]
思路
前缀和数组的变形,本质是一样的。
我们新建一个数组 nums 存储 arr[0:i] 的异或和
- 比如
nums[2]就是0 ^ arr[0] ^ arr[1] - 比如
nums[3]就是0 ^ arr[0] ^ arr[1] ^ arr[2]
那么我们想知道从 arr[l] 一直异或到 arr[r] 的和,只需要拿 nums[r + 1] ^ nums[l]
实现了一次遍历,多次求子数组的异或和。
代码
function xorQueries(arr: number[], queries: number[][]): number[] {
const n = arr.length
const nums = new Array(n+1).fill(0)
for (let i = 0; i < n; i++) {
nums[i+1] = nums[i] ^ arr[i]
}
const res = []
for (let [x, y] of queries) {
res.push(nums[x] ^ nums[y + 1])
}
return res
};
5.11
数学题?脑筋急转弯?
题目
1734. 解码异或后的排列
难度中等
给你一个整数数组
perm,它是前n个正整数的排列,且n是个 奇数 。它被加密成另一个长度为
n - 1的整数数组encoded,满足encoded[i] = perm[i] XOR perm[i + 1]。比方说,如果perm = [1,3,2],那么encoded = [2,1]。给你
encoded数组,请你返回原始数组perm。题目保证答案存在且唯一。示例 1:
输入:encoded = [3,1] 输出:[1,2,3] 解释:如果 perm = [1,2,3] ,那么 encoded = [1 XOR 2,2 XOR 3] = [3,1]示例 2:
输入:encoded = [6,5,4,6] 输出:[2,4,1,5,3]
思路
参考题解
- 将
encoded数组的奇数位上的数字逐个异或,其结果就等于原数组perm中的前n-1个数字异或的结果。 - 将
1-n进行异或,其结果等于原数组perm中所有数字异或的结果。 - 将以上两个结果求异或,即可求出
perm数组中的最后一个数字。 - 利用该数字和
encoded数字进行迭代异或,即可求出最后结果。
代码
function decode(encoded: number[]): number[] {
let n = encoded.length + 1
// 求 perm[0:n-1] 的异或结果
let last = 0
for(let i = 0; i < n; i += 2) {
last ^= encoded[i]
}
// 求 [1:n] 的异或结果
for(let i = 1; i <= n; i++) {
last ^= i
}
// 此时已知原数组最后一个数为 last
const perm = new Array(n).fill(0)
perm[n-1] = last
for(let i = n - 2; i >= 0; i--) {
perm[i] = perm[i+1] ^ encoded[i]
}
return perm
};
5.10
简单题,重拳出击👊
题目
872. 叶子相似的树
难度简单
请考虑一棵二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。
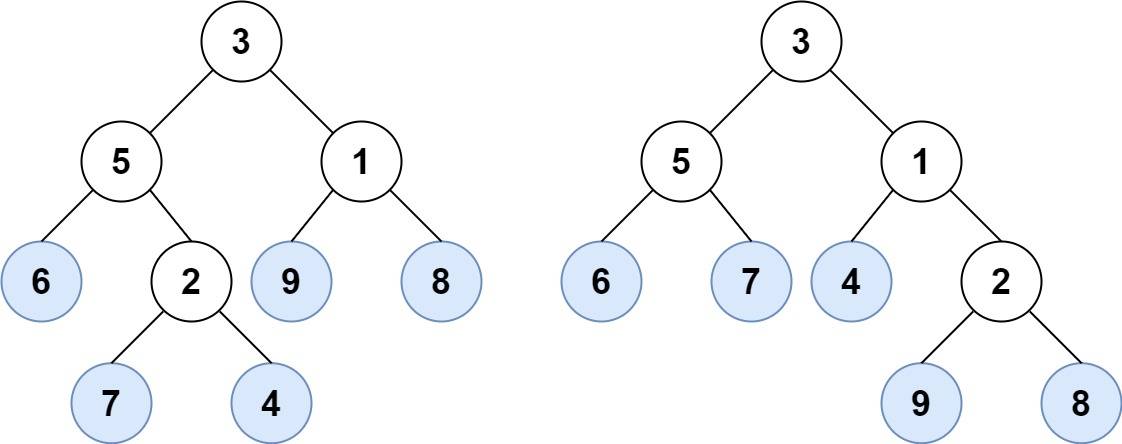
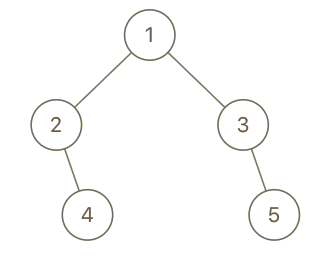
举个例子,如上图所示,给定一棵叶值序列为
(6, 7, 4, 9, 8)的树。如果有两棵二叉树的叶值序列是相同,那么我们就认为它们是 叶相似 的。
如果给定的两个根结点分别为
root1和root2的树是叶相似的,则返回true;否则返回false。示例 1:

输入:root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8] 输出:true
思路
深搜获取所有的叶子的值,然后比较两棵树的值是否相等。
代码
/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function leafSimilar(root1: TreeNode | null, root2: TreeNode | null): boolean {
const nodes1 = [], nodes2 = []
const dfs = (node: TreeNode, nodes: number[]) => {
if (!node.left && !node.right) {
nodes.push(node.val)
}
if (node.left) {
dfs(node.left, nodes)
}
if (node.right) {
dfs(node.right, nodes)
}
}
dfs(root1, nodes1)
dfs(root2, nodes2)
if (nodes1.length !== nodes2.length) return false
return nodes1.every((val, ind) => val === nodes2[ind])
};
5.9
题目
1482. 制作 m 束花所需的最少天数
难度中等
给你一个整数数组
bloomDay,以及两个整数m和k。现需要制作
m束花。制作花束时,需要使用花园中 相邻的k朵花 。花园中有
n朵花,第i朵花会在bloomDay[i]时盛开,恰好 可以用于 一束 花中。请你返回从花园中摘
m束花需要等待的最少的天数。如果不能摘到m束花则返回 -1 。示例 1:
输入:bloomDay = [1,10,3,10,2], m = 3, k = 1 输出:3 解释:让我们一起观察这三天的花开过程,x 表示花开,而 _ 表示花还未开。 现在需要制作 3 束花,每束只需要 1 朵。 1 天后:[x, _, _, _, _] // 只能制作 1 束花 2 天后:[x, _, _, _, x] // 只能制作 2 束花 3 天后:[x, _, x, _, x] // 可以制作 3 束花,答案为 3示例 2:
输入:bloomDay = [1,10,3,10,2], m = 3, k = 2 输出:-1 解释:要制作 3 束花,每束需要 2 朵花,也就是一共需要 6 朵花。而花园中只有 5 朵花,无法满足制作要求,返回 -1 。示例 3:
输入:bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3 输出:12 解释:要制作 2 束花,每束需要 3 朵。 花园在 7 天后和 12 天后的情况如下: 7 天后:[x, x, x, x, _, x, x] 可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花,因为它们不相邻。 12 天后:[x, x, x, x, x, x, x] 显然,我们可以用不同的方式制作两束花。示例 4:
输入:bloomDay = [1000000000,1000000000], m = 1, k = 1 输出:1000000000 解释:需要等 1000000000 天才能采到花来制作花束示例 5:
输入:bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2 输出:9
思路
直接用二分是我没想到的。
代码
function minDays(bloomDay: number[], m: number, k: number): number {
let n = bloomDay.length
if (m * k > n) {
return -1
}
const check = (days: number) => {
// 检查过了 days 天能否完成任务
let pre = 0, cnt = 0
bloomDay.map((day) => {
if (day <= days) {
pre += 1
if (pre === k) {
pre = 0
cnt += 1
}
} else {
pre = 0
}
})
return cnt >= m
}
let left = 0, right = Math.max(...bloomDay)
while (left < right) {
const mid = Math.floor((left + right) / 2)
if (check(mid)) {
right = mid
} else {
left = mid + 1
}
}
return left
};
5.8
题目
1723. 完成所有工作的最短时间
难度困难
给你一个整数数组
jobs,其中jobs[i]是完成第i项工作要花费的时间。请你将这些工作分配给
k位工人。所有工作都应该分配给工人,且每项工作只能分配给一位工人。工人的 工作时间 是完成分配给他们的所有工作花费时间的总和。请你设计一套最佳的工作分配方案,使工人的 最大工作时间 得以 最小化 。返回分配方案中尽可能 最小 的 最大工作时间 。
示例 1:
输入:jobs = [3,2,3], k = 3 输出:3 解释:给每位工人分配一项工作,最大工作时间是 3 。示例 2:
输入:jobs = [1,2,4,7,8], k = 2 输出:11 解释:按下述方式分配工作: 1 号工人:1、2、8(工作时间 = 1 + 2 + 8 = 11) 2 号工人:4、7(工作时间 = 4 + 7 = 11) 最大工作时间是 11 。
思路
困难折磨题,参考题解
DFS + 剪枝
本质上深搜,逐个安排任务,并且更新个人最长工作时间。
优化两点:
- 如果当前的个人最大工作时长已经超过了之前找到的可能答案,则退出递归。
- 尽可能把工作安排给没有工作的人。
代码
function minimumTimeRequired(jobs: number[], k: number): number {
const n = jobs.length
let times = new Array(k).fill(0) // times[i] 表示第 i 个工人的工作时间
let res = Number.MAX_SAFE_INTEGER
const dfs = (idx, times, max, used) => {
if (max >= res) {
return
}
if (idx === n) {
res = max
return
}
// 优先分配空闲工人
if (used < k) {
times[used] = jobs[idx]
dfs(idx + 1, times, Math.max(times[used], max), used + 1)
times[used] = 0
}
for (let i = 0; i < used; i++) {
times[i] += jobs[idx]
dfs(idx + 1, times, Math.max(times[i], max), used)
times[i] -= jobs[idx]
}
}
dfs(0, times, 0, 0)
return res
};
5.7
题目
1486. 数组异或操作
难度简单
给你两个整数,
n和start。数组
nums定义为:nums[i] = start + 2*i(下标从 0 开始)且n == nums.length。请返回
nums中所有元素按位异或(XOR)后得到的结果。示例 1:
输入:n = 5, start = 0 输出:8 解释:数组 nums 为 [0, 2, 4, 6, 8],其中 (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8 。 "^" 为按位异或 XOR 运算符。
思路
别问,问就是模拟。
代码
模拟
function xorOperation(n: number, start: number): number {
let res = start
for (let i = 1; i < n; i++) {
res ^= (start + 2 * i)
}
return res
};
5.6
题目
1720. 解码异或后的数组
难度简单
未知 整数数组
arr由n个非负整数组成。经编码后变为长度为
n - 1的另一个整数数组encoded,其中encoded[i] = arr[i] XOR arr[i + 1]。例如,arr = [1,0,2,1]经编码后得到encoded = [1,2,3]。给你编码后的数组
encoded和原数组arr的第一个元素first(arr[0])。请解码返回原数组
arr。可以证明答案存在并且是唯一的。示例 1:
输入:encoded = [1,2,3], first = 1 输出:[1,0,2,1] 解释:若 arr = [1,0,2,1] ,那么 first = 1 且 encoded = [1 XOR 0, 0 XOR 2, 2 XOR 1] = [1,2,3]示例 2:
输入:encoded = [6,2,7,3], first = 4 输出:[4,2,0,7,4]
思路
利用异或的特性 x ^ y ^ x = y,逐个恢复被编码后的数字。
代码
function decode(encoded: number[], first: number): number[] {
const arr = [first, ...encoded]
for(let i = 1; i < arr.length; i++) {
arr[i] ^= arr[i - 1]
}
return arr
};
5.5
假期结束啦,回来继续动规了
题目
740. 删除并获得点数
难度中等
给你一个整数数组
nums,你可以对它进行一些操作。每次操作中,选择任意一个
nums[i],删除它并获得nums[i]的点数。之后,你必须删除每个等于nums[i] - 1或nums[i] + 1的元素。开始你拥有
0个点数。返回你能通过这些操作获得的最大点数。示例 1:
输入:nums = [3,4,2] 输出:6 解释: 删除 4 获得 4 个点数,因此 3 也被删除。 之后,删除 2 获得 2 个点数。总共获得 6 个点数。示例 2:
输入:nums = [2,2,3,3,3,4] 输出:9 解释: 删除 3 获得 3 个点数,接着要删除两个 2 和 4 。 之后,再次删除 3 获得 3 个点数,再次删除 3 获得 3 个点数。 总共获得 9 个点数。提示:
1 <= nums.length <= 2 * 1041 <= nums[i] <= 104
思路
看了题解发现就跟打家劫舍动规实际上是一个思路。
首先用哈希表计数,因为 每个数字的价值 = 数字大小 * 出现次数
然后对数组进行去重和排序,从最小的数字开始看,比较删除当前数字和不删除当前数字的情况的最大分数。
当然这里如果这个数字和上一个数字不相同,则不需要删,将当前分数直接和上一个数的最大分数相加即可。
代码
function deleteAndEarn(nums: number[]): number {
// 计数
const map = new Map()
for(let i of nums) {
if (map.has(i)) {
map.set(i, map.get(i) + 1)
} else {
map.set(i, 1)
}
}
// 排序
nums.sort((x, y) => x - y)
const sortedNums = Array.from(new Set(nums))
const n = sortedNums.length
// 动态规划
const dp = new Array(n + 1).fill(0)
dp[1] = map.get(sortedNums[0]) * sortedNums[0]
for(let i = 1; i < n; i++) {
let num = sortedNums[i]
if (num == sortedNums[i-1] + 1) {
// 数字相连必须删
dp[i + 1] = Math.max(dp[i], dp[i - 1] + map.get(num) * num)
} else {
// 不相连直接加
dp[i + 1] = dp[i] + map.get(num) * num
}
}
return dp[n]
};