2021年1月刷题日志
2.4
美赛前的最后一天寒假了
题目
643. 子数组最大平均数 I
难度简单
给定
n个整数,找出平均数最大且长度为k的连续子数组,并输出该最大平均数。示例:
输入:[1,12,-5,-6,50,3], k = 4 输出:12.75 解释:最大平均数 (12-5-6+50)/4 = 51/4 = 12.75提示:
- 1 <=
k<=n<= 30,000。- 所给数据范围 [-10,000,10,000]。
思路
没啥花里胡哨的,用滑动窗口模拟就行
代码
class Solution:
def findMaxAverage(self, nums: List[int], k: int) -> float:
cur_sum = 0
for i in range(k-1):
cur_sum += nums[i]
cur_max = -float('inf')
for i in range(k-1,len(nums)):
cur_sum += nums[i]
cur_max = max(cur_max, cur_sum)
cur_sum -= nums[i-k+1]
return cur_max/k
2.3
题目
480. 滑动窗口中位数
难度困难
中位数是有序序列最中间的那个数。如果序列的大小是偶数,则没有最中间的数;此时中位数是最中间的两个数的平均数。
例如:
[2,3,4],中位数是3[2,3],中位数是(2 + 3) / 2 = 2.5给你一个数组 nums,有一个大小为 k 的窗口从最左端滑动到最右端。窗口中有 k 个数,每次窗口向右移动 1 位。你的任务是找出每次窗口移动后得到的新窗口中元素的中位数,并输出由它们组成的数组。
示例:
给出 nums =
[1,3,-1,-3,5,3,6,7],以及 k = 3。窗口位置 中位数 --------------- ----- [1 3 -1] -3 5 3 6 7 1 1 [3 -1 -3] 5 3 6 7 -1 1 3 [-1 -3 5] 3 6 7 -1 1 3 -1 [-3 5 3] 6 7 3 1 3 -1 -3 [5 3 6] 7 5 1 3 -1 -3 5 [3 6 7] 6因此,返回该滑动窗口的中位数数组
[1,-1,-1,3,5,6]。提示:
- 你可以假设
k始终有效,即:k始终小于输入的非空数组的元素个数。- 与真实值误差在
10 ^ -5以内的答案将被视作正确答案。
思路
暴力法
代码
class Solution:
def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:
n = len(nums)
res = []
for i in range(n-k+1):
tmp = nums[i:i+k]
tmp.sort()
if len(tmp)%2 == 1:
res.append(tmp[k//2])
else:
res.append((tmp[k//2]+tmp[k//2-1])/2)
return res
2.2
题目
424. 替换后的最长重复字符
难度中等
给你一个仅由大写英文字母组成的字符串,你可以将任意位置上的字符替换成另外的字符,总共可最多替换 k 次。在执行上述操作后,找到包含重复字母的最长子串的长度。
**注意:**字符串长度 和 k 不会超过 104。
示例 1:
输入:s = "ABAB", k = 2 输出:4 解释:用两个'A'替换为两个'B',反之亦然。示例 2:
输入:s = "AABABBA", k = 1 输出:4 解释: 将中间的一个'A'替换为'B',字符串变为 "AABBBBA"。 子串 "BBBB" 有最长重复字母, 答案为 4。
思路
双指针,滑动窗口,遍历字符串,用一个数组来维护窗口中字母的出现次数
代码
class Solution:
def characterReplacement(self, s: str, k: int) -> int:
cnts = [0]*26
left = right = maxn = 0
n = len(s)
while right < n:
cnts[ord(s[right]) - ord('A')] += 1
maxn = max(maxn, cnts[ord(s[right]) - ord('A')])
if right - left + 1 - maxn > k:
cnts[ord(s[left]) - ord('A')] -= 1
left += 1
right += 1
return right - left
2.1
今日简单题,刷完吃寿喜烧去咯
题目
888. 公平的糖果棒交换
难度简单99
爱丽丝和鲍勃有不同大小的糖果棒:
A[i]是爱丽丝拥有的第i根糖果棒的大小,B[j]是鲍勃拥有的第j根糖果棒的大小。因为他们是朋友,所以他们想交换一根糖果棒,这样交换后,他们都有相同的糖果总量。(一个人拥有的糖果总量是他们拥有的糖果棒大小的总和。)
返回一个整数数组
ans,其中ans[0]是爱丽丝必须交换的糖果棒的大小,ans[1]是 Bob 必须交换的糖果棒的大小。如果有多个答案,你可以返回其中任何一个。保证答案存在。
示例 1:
输入:A = [1,1], B = [2,2] 输出:[1,2]示例 2:
输入:A = [1,2], B = [2,3] 输出:[1,2]示例 3:
输入:A = [2], B = [1,3] 输出:[2,3]示例 4:
输入:A = [1,2,5], B = [2,4] 输出:[5,4]提示:
1 <= A.length <= 100001 <= B.length <= 100001 <= A[i] <= 1000001 <= B[i] <= 100000- 保证爱丽丝与鲍勃的糖果总量不同。
- 答案肯定存在。
思路
traversing and binary search.
代码
class Solution:
def fairCandySwap(self, A: List[int], B: List[int]) -> List[int]:
sum_a = sum(A)
sum_b = sum(B)
diff = sum_a-sum_b
for i in A:
j = int(i-diff/2)
if j in B:
return [i,j]
1.31
可恶啊,昨天看到是困难题,甚至CV都给忘了
今天又是并查集
题目
839. 相似字符串组
难度困难
如果交换字符串
X中的两个不同位置的字母,使得它和字符串Y相等,那么称X和Y两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。例如,
"tars"和"rats"是相似的 (交换0与2的位置);"rats"和"arts"也是相似的,但是"star"不与"tars","rats",或"arts"相似。总之,它们通过相似性形成了两个关联组:
{"tars", "rats", "arts"}和{"star"}。注意,"tars"和"arts"是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。给你一个字符串列表
strs。列表中的每个字符串都是strs中其它所有字符串的一个字母异位词。请问strs中有多少个相似字符串组?示例 1:
输入:strs = ["tars","rats","arts","star"] 输出:2示例 2:
输入:strs = ["omv","ovm"] 输出:1提示:
1 <= strs.length <= 1001 <= strs[i].length <= 1000sum(strs[i].length) <= 2 * 104strs[i]只包含小写字母。strs中的所有单词都具有相同的长度,且是彼此的字母异位词。
思路
题目难度虽然是困难,但是其实具体的实现还是很简单的。
参考了官方题解之后豁然开朗,这道题目其实还是一个传统的并查集题目。
首先看到了我们的最终目标是求相似字符串组,其实就是抽象成并查集里的连通情况。
两个字符串相似,就说明是两个字符串相连(union)。
所以我们只需要维护一个并查集,遍历不同字符串组合确认是否连通,最后输出连通分量的个数即可。
维护并查集很简单,就是纯粹的最简单的模板。
确认字符串的相似性也不难,实现方法应该有很多,我这边就比较随意地写了一个。
- 我们手上有两个字符串
str1,str2 - 题目的条件是已知这两个字符串长度相等,因此我们直接按照位置来遍历字符串即可
- 新建一个数组
diff_chars,用来存放不同这两个字符串中的同一个位置上的不同的字符对(x_i, y_i),表示第i个位置上的两个不同字符。 - 同时遍历完两个字符串之后,我们去判断
diff_chars的长度,只有当长度为的2 的时候,我们才能确认两个字符串有可能相似(在一开始的时候我们就提前判断字符串是否相等) - 相似还需要确认字符对调之后是相同,因此对比一下数组中的两个字符对即可
代码
class UnionFind:
def __init__(self, n):
self.parents = list(range(n))
self.cnt = n
def find(self, x):
if self.parents[x] != x:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
f_x, f_y = self.find(x), self.find(y)
if f_x != f_y:
self.parents[f_x] = f_y
self.cnt -= 1
class Solution:
def numSimilarGroups(self, strs: List[str]) -> int:
n = len(strs)
uf = UnionFind(n)
def is_similar(str1, str2):
# 对比两个字符串是否相似
if str1 == str2:
return True
diff_chars = []
for i in range(len(str1)):
if str1[i] != str2[i]:
diff_chars.append((str1[i], str2[i]))
if len(diff_chars)!=2:
return False
a, b = diff_chars[0]
c, d = diff_chars[1]
if a==d and b==c:
return True
else:
return False
for i in range(0, n-1):
for j in range(i+1, n):
# 两两对比 确认相似
str1, str2 = strs[i], strs[j]
if uf.find(i) != uf.find(j):
if is_similar(str1, str2):
uf.union(i,j)
return uf.cnt
1.29
题目
1631. 最小体力消耗路径
难度中等
你准备参加一场远足活动。给你一个二维
rows x columns的地图heights,其中heights[row][col]表示格子(row, col)的高度。一开始你在最左上角的格子(0, 0),且你希望去最右下角的格子(rows-1, columns-1)(注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
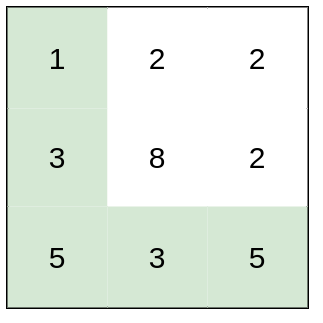
输入:heights = [[1,2,2],[3,8,2],[5,3,5]] 输出:2 解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。 这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。示例 2:
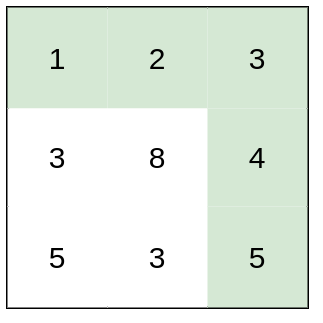
输入:heights = [[1,2,3],[3,8,4],[5,3,5]] 输出:1 解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。示例 3:
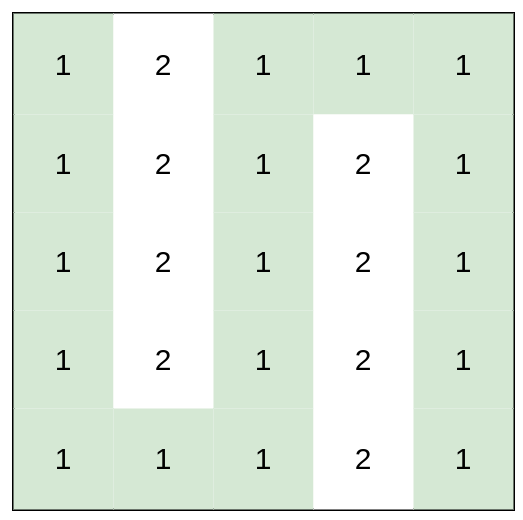
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]] 输出:0 解释:上图所示路径不需要消耗任何体力。提示:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 106
思路
需要抽象成图,每个格子代表一个结点,格子与格子之间的差值的绝对值就是边的权值。
题解中提供了三种思路
- 二分法
- 并查集
- Dijkstra 最短路径
学习了一下 Dijkstra 最短路径算法,简单来说就是启发式搜索,一个利用启发函数的 BFS
维护一个小顶堆 q,维护一个遍历过的结点集合 visited,维护一个最短路径长度表 dist。
-
每次遍历的时候找到当前小顶堆中代价最小的,即所需消耗体力最少的。
-
向四周遍历,假设从当前结点出发到达下一个结点的代价比
dist的中的值小,则替换,并加入小顶堆,以便下一次可以遍历 -
遍历的时候需要确保当前结点未被遍历过
-
直到走到终点,即可退出遍历
代码
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
# dijkstra
m, n = len(heights), len(heights[0])
dist = [0]+[float('inf')]*(m*n-1)
visited = set()
q = [(0,0,0)]
while q:
d, x, y = heapq.heappop(q)
node = x*n + y
if node in visited:
continue
if (x,y) == (m-1,n-1):
break
visited.add(node)
for nx, ny in [(x-1,y),(x+1,y),(x,y-1),(x,y+1)]:
if 0<=nx<m and 0<=ny<n and max(d, abs(heights[x][y]-heights[nx][ny]))<=dist[nx*n+ny]:
dist[nx*n+ny] = max(d, abs(heights[x][y]-heights[nx][ny]))
heapq.heappush(q, (dist[nx * n + ny], nx, ny))
return dist[m*n - 1]
1.28
昨日困难题又CV了,惭愧
题目
724. 寻找数组的中心索引
难度简单
给定一个整数类型的数组
nums,请编写一个能够返回数组 “中心索引” 的方法。我们是这样定义数组 中心索引 的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
如果数组不存在中心索引,那么我们应该返回 -1。如果数组有多个中心索引,那么我们应该返回最靠近左边的那一个。
示例 1:
输入: nums = [1, 7, 3, 6, 5, 6] 输出:3 解释: 索引 3 (nums[3] = 6) 的左侧数之和 (1 + 7 + 3 = 11),与右侧数之和 (5 + 6 = 11) 相等。 同时, 3 也是第一个符合要求的中心索引。示例 2:
输入: nums = [1, 2, 3] 输出:-1 解释: 数组中不存在满足此条件的中心索引。说明:
nums的长度范围为[0, 10000]。- 任何一个
nums[i]将会是一个范围在[-1000, 1000]的整数。
思路
维护一个当前求得的和,遍历数组找中心索引
代码
class Solution:
def pivotIndex(self, nums: List[int]) -> int:
cur_sum = 0
if len(nums)==1: return 0
tot = sum(nums)
for i,num in enumerate(nums):
target = tot-cur_sum-nums[i]
if cur_sum == target:
return i
cur_sum += num
return -1
1.26
简单题,好耶(然而我却WA了)
题目
1128. 等价多米诺骨牌对的数量
难度简单
给你一个由一些多米诺骨牌组成的列表
dominoes。如果其中某一张多米诺骨牌可以通过旋转
0度或180度得到另一张多米诺骨牌,我们就认为这两张牌是等价的。形式上,
dominoes[i] = [a, b]和dominoes[j] = [c, d]等价的前提是a==c且b==d,或是a==d且b==c。在
0 <= i < j < dominoes.length的前提下,找出满足dominoes[i]和dominoes[j]等价的骨牌对(i, j)的数量。示例:
输入:dominoes = [[1,2],[2,1],[3,4],[5,6]] 输出:1提示:
1 <= dominoes.length <= 400001 <= dominoes[i][j] <= 9
思路
用数组模拟哈希表进行计数
代码
class Solution:
def numEquivDominoPairs(self, dominoes: List[List[int]]) -> int:
nums = [0]*100
cnt = 0
for i, j in dominoes:
k = i*10+j if i>j else j*10+i
cnt += nums[k]
nums[k] += 1
return cnt
1.25
我的天,原来我鸽了4天吗
新的建模题太折磨了🤕
题目
959. 由斜杠划分区域
难度中等
在由 1 x 1 方格组成的 N x N 网格
grid中,每个 1 x 1 方块由/、\或空格构成。这些字符会将方块划分为一些共边的区域。(请注意,反斜杠字符是转义的,因此
\用"\\"表示。)。返回区域的数目。
示例 1:
输入: [ " /", "/ " ] 输出:2 解释:2x2 网格如下:示例 2:
输入: [ " /", " " ] 输出:1 解释:2x2 网格如下:示例 3:
输入: [ "\\/", "/\\" ] 输出:4 解释:(回想一下,因为 \ 字符是转义的,所以 "\\/" 表示 \/,而 "/\\" 表示 /\。) 2x2 网格如下:示例 4:
输入: [ "/\\", "\\/" ] 输出:5 解释:(回想一下,因为 \ 字符是转义的,所以 "/\\" 表示 /\,而 "\\/" 表示 \/。) 2x2 网格如下:示例 5:
输入: [ "//", "/ " ] 输出:3 解释:2x2 网格如下:提示:
1 <= grid.length == grid[0].length <= 30grid[i][j]是'/'、'\'、或' '。
思路
参考了官方题解,是很巧妙的并查集解法
本身用并查集求连通度不难,但是要发现怎么去划分区域就有点…
借用官方的图来说,每个格子划分成4块,分别对应0, 1, 2, 3
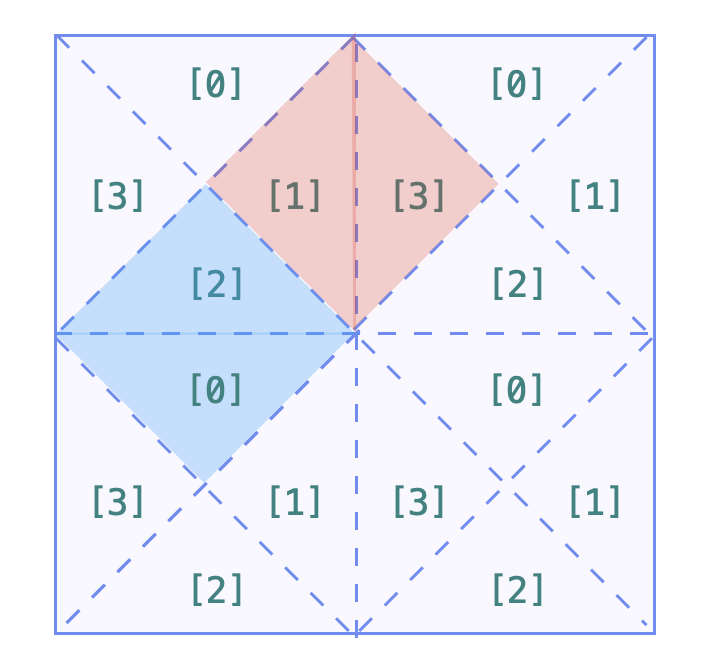
我们可以把整个大的正方形抽象成一个4*N*N的数组,数组的每个元素代表的是四分之一个小正方形
因此,我们的并查集大小也是4*N*N,一开始假设都不是连通的
遍历grid的矩阵,相当于我们每次对一个小正方形内的四块进行操作
每次要进行的有两个操作
- 小正方形内合并
- 小正方形间合并
针对正方形内合并
- 如果遍历到的是空格,即
‘ ’,就把方块内四个格子全部连通 - 如果遍历到的是
/,就把1和2连通,0和3连通 - 如果遍历到的是
\\,就把0和1连通,2和3连通
针对正方形间合并
- 右侧合并
- 将当前块的1和右侧块的3合并
- 下侧合并
- 将当前块的2和下侧块的0合并
1.20
不知不觉都20号了
题目
628. 三个数的最大乘积
难度简单242
给定一个整型数组,在数组中找出由三个数组成的最大乘积,并输出这个乘积。
示例 1:
输入: [1,2,3] 输出: 6示例 2:
输入: [1,2,3,4] 输出: 24注意:
- 给定的整型数组长度范围是[3,104],数组中所有的元素范围是[-1000, 1000]。
- 输入的数组中任意三个数的乘积不会超出32位有符号整数的范围。
思路
今天的题可太简单了,先排序,然后最大的乘积只可能是以下两个乘积之一
- 最大的三个数的乘积
- 最小的两个数和最大的一个数的乘积
代码
class Solution:
def maximumProduct(self, nums: List[int]) -> int:
nums.sort()
res =[]
res.append(nums[0]*nums[1]*nums[-1])
res.append(nums[-1]*nums[-2]*nums[-3])
return max(res)
1.19
龙妈的三条龙可太折磨了。
题目
1584. 连接所有点的最小费用
难度中等
给你一个
points数组,表示 2D 平面上的一些点,其中points[i] = [xi, yi]。连接点
[xi, yi]和点[xj, yj]的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj|,其中|val|表示val的绝对值。请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
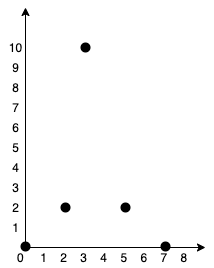
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]] 输出:20 解释: 我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 注意到任意两个点之间只有唯一一条路径互相到达。示例 2:
输入:points = [[3,12],[-2,5],[-4,1]] 输出:18示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]] 输出:4示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]] 输出:4000000示例 5:
输入:points = [[0,0]] 输出:0提示:
1 <= points.length <= 1000-106 <= xi, yi <= 106- 所有点
(xi, yi)两两不同。
思路
关键词:并查集,Kruskal算法,最小生成树
- 确定N个点之间所有可能的边
- 对所有边排序,升序排序
- 从最小的边开始遍历
- 如果遍历到的边连接到的是两个未连通的结点,则生成该条边
- 直到所有的点都连通
代码
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
n = len(points)
parents = list(range(n))
def find(x):
if x != parents[x]:
parents[x] = find(parents[x])
return parents[x]
dist = []
for i in range(n-1):
x1,y1 = points[i]
for j in range(i+1,n):
x2,y2 = points[j]
dist.append([i,j,abs(x2-x1)+abs(y2-y1)])
dist.sort(key = lambda x: x[2])
# 构建最小生成树
edge, cost = 0, 0
for i,j,d in dist:
a, b = find(i), find(j)
if a != b:
# 两个点不连通
edge += 1
cost += d
parents[b] = a
if edge == n-1:
return cost
return cost
1.18
怎么寒假了还要这么头秃
题目
721. 账户合并
难度中等
给定一个列表
accounts,每个元素accounts[i]是一个字符串列表,其中第一个元素accounts[i][0]是 名称 (name),其余元素是 emails 表示该账户的邮箱地址。现在,我们想合并这些账户。如果两个账户都有一些共同的邮箱地址,则两个账户必定属于同一个人。请注意,即使两个账户具有相同的名称,它们也可能属于不同的人,因为人们可能具有相同的名称。一个人最初可以拥有任意数量的账户,但其所有账户都具有相同的名称。
合并账户后,按以下格式返回账户:每个账户的第一个元素是名称,其余元素是按顺序排列的邮箱地址。账户本身可以以任意顺序返回。
示例 1:
输入: accounts = [["John", "johnsmith@mail.com", "john00@mail.com"], ["John", "johnnybravo@mail.com"], ["John", "johnsmith@mail.com", "john_newyork@mail.com"], ["Mary", "mary@mail.com"]] 输出: [["John", 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com'], ["John", "johnnybravo@mail.com"], ["Mary", "mary@mail.com"]] 解释: 第一个和第三个 John 是同一个人,因为他们有共同的邮箱地址 "johnsmith@mail.com"。 第二个 John 和 Mary 是不同的人,因为他们的邮箱地址没有被其他帐户使用。 可以以任何顺序返回这些列表,例如答案 [['Mary','mary@mail.com'],['John','johnnybravo@mail.com'], ['John','john00@mail.com','john_newyork@mail.com','johnsmith@mail.com']] 也是正确的。提示:
accounts的长度将在[1,1000]的范围内。accounts[i]的长度将在[1,10]的范围内。accounts[i][j]的长度将在[1,30]的范围内。
思路
我以为是单纯的两个哈希表能解决,结果一看题解又是并查集
-
一个哈希表存储:邮箱->index
-
另一个哈希表存储:邮箱->人名
利用第一个哈希表,把同一个人的邮箱用并查集连通在一起
比如 x@x.com 如果和 y@y.com 是同一个人的,那么就连结到一个公共的父节点上去(这里用index表示父节点)
连接完之后,它们的index就相同了
最后利用第二个哈希表,把index相同的邮箱,放到同一个人名下,即可
代码
class Solution:
def accountsMerge(self, accounts: List[List[str]]) -> List[List[str]]:
email_to_index = dict()
email_to_name = dict()
for account in accounts:
name = account[0]
for email in account[1:]:
if email not in email_to_index:
email_to_index[email] = len(email_to_index)
email_to_name[email] = name
n = len(email_to_index)
parents = list(range(n))
def find(x):
if parents[x] != x:
parents[x] = find(parents[x])
return parents[x]
def union(x,y):
f_x, f_y = find(x), find(y)
if f_x != f_y:
parents[f_x] = f_y
# 开始合并同一个人的邮箱
for account in accounts:
first_index = email_to_index[account[1]]
for email in account[2:]:
union(first_index, email_to_index[email])
index_to_emails = collections.defaultdict(list)
for email, index in email_to_index.items():
index = find(index)
index_to_emails[index].append(email)
res = []
for emails in index_to_emails.values():
res.append([email_to_name[emails[0]]] + sorted(emails))
return res
1.17
赶紧刷完题建模去了(这次培训竟然第一道就是对龙妈的三条🐉去建模)
题目
1232. 缀点成线
难度简单
在一个 XY 坐标系中有一些点,我们用数组
coordinates来分别记录它们的坐标,其中coordinates[i] = [x, y]表示横坐标为x、纵坐标为y的点。请你来判断,这些点是否在该坐标系中属于同一条直线上,是则返回
true,否则请返回false。示例 1:
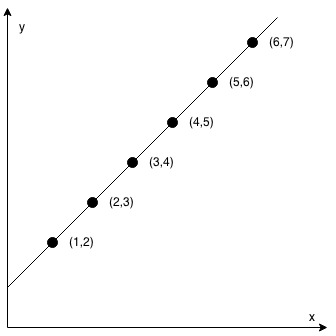
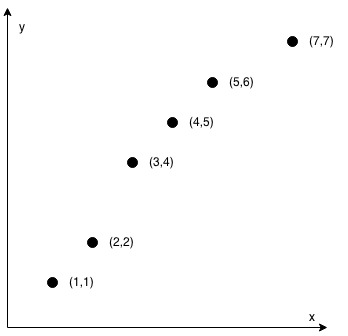
输入:coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]] 输出:true示例 2:
输入:coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]] 输出:false提示:
2 <= coordinates.length <= 1000coordinates[i].length == 2-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4coordinates中不含重复的点
思路
啥技巧都没用,就直接算斜率
代码
class Solution:
def checkStraightLine(self, coordinates: List[List[int]]) -> bool:
x0, y0 = coordinates[0]
x1, y1 = coordinates[1]
if x1 == x0:
for x,y in coordinates[1:]:
if x!=x0:
return False
return True
else:
k = (y1-y0)/(x1-x0)
for x,y in coordinates[2:]:
if x==x0: return False
elif (y-y0)/(x-x0) != k:
return False
return True
1.16
打砖块,并查集,困难,放假,CV
1.15
放 假 啦!
题目
947. 移除最多的同行或同列石头
难度中等
n块石头放置在二维平面中的一些整数坐标点上。每个坐标点上最多只能有一块石头。如果一块石头的 同行或者同列 上有其他石头存在,那么就可以移除这块石头。
给你一个长度为
n的数组stones,其中stones[i] = [xi, yi]表示第i块石头的位置,返回 可以移除的石子 的最大数量。示例 1:
输入:stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]] 输出:5 解释:一种移除 5 块石头的方法如下所示: 1. 移除石头 [2,2] ,因为它和 [2,1] 同行。 2. 移除石头 [2,1] ,因为它和 [0,1] 同列。 3. 移除石头 [1,2] ,因为它和 [1,0] 同行。 4. 移除石头 [1,0] ,因为它和 [0,0] 同列。 5. 移除石头 [0,1] ,因为它和 [0,0] 同行。 石头 [0,0] 不能移除,因为它没有与另一块石头同行/列。示例 2:
输入:stones = [[0,0],[0,2],[1,1],[2,0],[2,2]] 输出:3 解释:一种移除 3 块石头的方法如下所示: 1. 移除石头 [2,2] ,因为它和 [2,0] 同行。 2. 移除石头 [2,0] ,因为它和 [0,0] 同列。 3. 移除石头 [0,2] ,因为它和 [0,0] 同行。 石头 [0,0] 和 [1,1] 不能移除,因为它们没有与另一块石头同行/列。示例 3:
输入:stones = [[0,0]] 输出:0 解释:[0,0] 是平面上唯一一块石头,所以不可以移除它。提示:
1 <= stones.length <= 10000 <= xi, yi <= 104- 不会有两块石头放在同一个坐标点上
思路
利用并查集,确定最后需要保留的点的个数
如果两个石头的行或者列相同,我们就可以认为它们是连通的
连通的石头意味着只需要留一块就够了
为了区分行和列,将行的值+10001
代码
class UnionFind:
def __init__(self,n):
self.dic = dict()
self.cnt = 0
def find(self, i):
if i not in self.dic:
self.dic[i] = i
self.cnt += 1
if self.dic[i] != i:
self.dic[i] = self.find(self.dic[i])
return self.dic[i]
def union(self, x, y):
f_x, f_y = self.find(x), self.find(y)
if f_x == f_y:
return
self.dic[f_x] = f_y
self.cnt -= 1
class Solution:
def removeStones(self, stones: List[List[int]]) -> int:
n = len(stones)
uf = UnionFind(n)
for i, j in stones:
uf.union(i+10001, j)
return n - uf.cnt
1.14
最后一门OS,给爷🐛!
题目
1018. 可被 5 整除的二进制前缀
难度简单
给定由若干
0和1组成的数组A。我们定义N_i:从A[0]到A[i]的第i个子数组被解释为一个二进制数(从最高有效位到最低有效位)。返回布尔值列表
answer,只有当N_i可以被5整除时,答案answer[i]为true,否则为false。示例 1:
输入:[0,1,1] 输出:[true,false,false] 解释: 输入数字为 0, 01, 011;也就是十进制中的 0, 1, 3 。只有第一个数可以被 5 整除,因此 answer[0] 为真。示例 2:
输入:[1,1,1] 输出:[false,false,false]示例 3:
输入:[0,1,1,1,1,1] 输出:[true,false,false,false,true,false]示例 4:
输入:[1,1,1,0,1] 输出:[false,false,false,false,false]提示:
1 <= A.length <= 30000A[i]为0或1
思路
全程只算余数即可
代码
class Solution:
def prefixesDivBy5(self, A: List[int]) -> List[bool]:
res = []
tmp = 0
for i in A:
tmp *= 2
tmp += i
tmp %= 5
if tmp == 0:
res.append(True)
else:
res.append(False)
return res
1.13
又是并查集😓
明天考OS,紧张到起飞
题目
684. 冗余连接
难度中等
在本问题中, 树指的是一个连通且无环的无向图。
输入一个图,该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间,这条附加的边不属于树中已存在的边。
结果图是一个以
边组成的二维数组。每一个边的元素是一对[u, v],满足u < v,表示连接顶点u和v的无向图的边。返回一条可以删去的边,使得结果图是一个有着N个节点的树。如果有多个答案,则返回二维数组中最后出现的边。答案边
[u, v]应满足相同的格式u < v。示例 1:
输入: [[1,2], [1,3], [2,3]] 输出: [2,3] 解释: 给定的无向图为: 1 / \ 2 - 3示例 2:
输入: [[1,2], [2,3], [3,4], [1,4], [1,5]] 输出: [1,4] 解释: 给定的无向图为: 5 - 1 - 2 | | 4 - 3注意:
- 输入的二维数组大小在 3 到 1000。
- 二维数组中的整数在1到N之间,其中N是输入数组的大小。
思路
用并查集确认两个结点是否连通(parent相同),如果在已经连通的情况下又有一条边将其相连,则说明产生了环路,返回这条边即可
代码
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
# 并查集
n = len(edges)
parents = list(range(n+1))
def find(i):
if parents[i] != i:
parents[i] = find(parents[i])
return parents[i]
def union(x,y):
fx, fy = find(x), find(y)
if fx!=fy:
parents[fx] = fy
for x,y in edges:
if find(x) == find(y):
return [x,y]
union(x,y)
1.12
图论,拓扑排序,困难题,cv
1.11
a lovely Monday.
题目
1202. 交换字符串中的元素
难度中等
给你一个字符串
s,以及该字符串中的一些「索引对」数组pairs,其中pairs[i] = [a, b]表示字符串中的两个索引(编号从 0 开始)。你可以 任意多次交换 在
pairs中任意一对索引处的字符。返回在经过若干次交换后,
s可以变成的按字典序最小的字符串。示例 1:
输入:s = "dcab", pairs = [[0,3],[1,2]] 输出:"bacd" 解释: 交换 s[0] 和 s[3], s = "bcad" 交换 s[1] 和 s[2], s = "bacd"示例 2:
输入:s = "dcab", pairs = [[0,3],[1,2],[0,2]] 输出:"abcd" 解释: 交换 s[0] 和 s[3], s = "bcad" 交换 s[0] 和 s[2], s = "acbd" 交换 s[1] 和 s[2], s = "abcd"示例 3:
输入:s = "cba", pairs = [[0,1],[1,2]] 输出:"abc" 解释: 交换 s[0] 和 s[1], s = "bca" 交换 s[1] 和 s[2], s = "bac" 交换 s[0] 和 s[1], s = "abc"提示:
1 <= s.length <= 10^50 <= pairs.length <= 10^50 <= pairs[i][0], pairs[i][1] < s.lengths中只含有小写英文字母
题目
初步复习了一下并查集(没有跟官方题解一样用按秩优化)
根据题目要求可以很快发现有一个连通子集的问题,比如[0,1]和[1,3]可以理解为在一个连通集合里
因此考虑用并查集实现快速地查询哪些元素是在一个集合里的
具体思路见代码,以及模板题解
代码实现使用的是递归的路径压缩(我还发现直接把并查集写在Solution里会报递归深度错误)
代码
class DSU:
def __init__(self, n:int):
self.p = [i for i in range(n)]
def find(self, x: int):
if x != self.p[x]:
self.p[x] = self.find(self.p[x])
return self.p[x]
def merge(self, x:int , y:int):
fx, fy = self.find(x), self.find(y)
if fx == fy: return
self.p[fx] = self.p[fy]
return
class Solution:
def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]) -> str:
# 构造并查集
length = len(s)
dsu = DSU(length)
for i,j in pairs:
dsu.merge(i,j)
dic = collections.defaultdict(list)
for i in range(length):
dic[dsu.find(i)].append(i)
res = list(range(length))
for v in dic.values():
words = [s[i] for i in v]
words.sort()
cnt = 0
v.sort()
for i in v:
res[i] = words[cnt]
cnt += 1
return "".join(res)
1.10
228. 汇总区间
难度简单
给定一个无重复元素的有序整数数组
nums。返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表。也就是说,
nums的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于nums的数字x。列表中的每个区间范围
[a,b]应该按如下格式输出:
"a->b",如果a != b
"a",如果a == b示例 1:
输入:nums = [0,1,2,4,5,7] 输出:["0->2","4->5","7"] 解释:区间范围是: [0,2] --> "0->2" [4,5] --> "4->5" [7,7] --> "7"示例 2:
输入:nums = [0,2,3,4,6,8,9] 输出:["0","2->4","6","8->9"] 解释:区间范围是: [0,0] --> "0" [2,4] --> "2->4" [6,6] --> "6" [8,9] --> "8->9"示例 3:
输入:nums = [] 输出:[]示例 4:
输入:nums = [-1] 输出:["-1"]示例 5:
输入:nums = [0] 输出:["0"]提示:
0 <= nums.length <= 20-231 <= nums[i] <= 231 - 1nums中的所有值都 互不相同nums按升序排列
思路
没有技术可言,就是遍历一遍数组,把所有连续的子数组转换成x->y的字符串即可
代码
class Solution:
def summaryRanges(self, nums: List[int]) -> List[str]:
if not nums:
return []
if len(nums) == 1:
return [str(nums[0])]
first, last = nums[0], nums[0]
res = []
for i,num in enumerate(nums[1:]):
if num != last + 1:
if first == last:
res.append(str(first))
else:
res.append(str(first)+"->"+str(last))
first = num
last = num
if i == len(nums)-2:
if first == last:
res.append(str(last))
else:
res.append(str(first)+"->"+str(last))
return res
1.9
@labuladong!yyds!
题解
123. 买卖股票的最佳时机 III
难度困难
给定一个数组,它的第
i个元素是一支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。 随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。示例 4:
输入:prices = [1] 输出:0提示:
1 <= prices.length <= 1050 <= prices[i] <= 105
思路
考完五门,还剩两门,计网和OS,还有四天,算是有空写题解了
看完东哥的算法小抄,真就直接秒杀动归呗。
一般来说,如果不限交易次数,只需要设置两个变量dp0和dp1分别表示当天未持有股票的状态和持有股票的状态。
这道题要求最多只能交易两次,所以我们的两个变量变成了两个数组
DP Table
-
dp0[i]表示当天未持有股票的最大利润,且已进行了i次交易(卖出过i次股票) -
dp1[i]表示当天持有股票的最大利润,且进行了i次交易
Base case
dp0 = [0,0,0],因为一开始未持有股票,所以第一天无论是交易了几次,最大利润都是0dp1 = [-float('inf'),-float('inf')],因为一开始不可能持有股票,所以我们初始化最大利润为负无穷(避免第一天就能卖股票)
状态转移方程
- 针对
dp0而言- 要么就是当天卖出了股票,要么就是本来就没有股票
dp0[0]永远为0,因为交易次数为0且未持有股票,说明从未购入股票dp0[1]为前一天未持有股票的最大收益,或者前一天持有股票且当天卖出股票的最大收益- 注意这里如果是保持未持有股票,则交易次数是不会变的
- 如果是卖出股票,那必定是根据
dp1[0]去更新的,因为更新后才变成dp0[1]所表示的1次交易
dp0[2]和dp0[1]同理
- 针对
dp1而言- 要么就是当天买入了股票,要么就是之前就持有了股票,还没卖
dp1[0]就是根据前一天已经持有股票的最大利润dp1[0],和当天买入股票的最大利润dp0[0]-pricedp1[1]同理,需要考虑交易次数
最后一天未持有股票,且交易次数为2的情况下必然是最大利益,即
dp0[2]
代码
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp0 = [0,0,0] # 表示当天未持有股票的情况
dp1 = [-float('inf'), -float('inf')] # 表示当天持有股票的情况
for price in prices:
dp0[1] = max(dp1[0]+price, dp0[1])
dp0[2] = max(dp1[1]+price, dp0[2])
dp1[0] = max(dp0[0]-price, dp1[0])
dp1[1] = max(dp0[1]-price, dp1[1])
return dp0[2]
1.8
软测老师捞捞我
题目
189. 旋转数组
难度中等
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: [1,2,3,4,5,6,7] 和 k = 3 输出: [5,6,7,1,2,3,4] 解释: 向右旋转 1 步: [7,1,2,3,4,5,6] 向右旋转 2 步: [6,7,1,2,3,4,5] 向右旋转 3 步: [5,6,7,1,2,3,4]示例 2:
输入: [-1,-100,3,99] 和 k = 2 输出: [3,99,-1,-100] 解释: 向右旋转 1 步: [99,-1,-100,3] 向右旋转 2 步: [3,99,-1,-100]说明:
- 尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
- 要求使用空间复杂度为 O(1) 的 原地 算法。
代码
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
k %= n
def reverse(i,j):
# 翻转数组的[i:j]
left, right = i, j-1
while left<right:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right -= 1
reverse(0,n)
reverse(0,k)
reverse(k,n)
1.7
真的复习不完了兄弟萌
题目
547. 省份数量
难度中等
有
n个城市,其中一些彼此相连,另一些没有相连。如果城市a与城市b直接相连,且城市b与城市c直接相连,那么城市a与城市c间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个
n x n的矩阵isConnected,其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连,而isConnected[i][j] = 0表示二者不直接相连。返回矩阵中 省份 的数量。
示例 1:
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]] 输出:2示例 2:
输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]] 输出:3提示:
1 <= n <= 200n == isConnected.lengthn == isConnected[i].lengthisConnected[i][j]为1或0isConnected[i][i] == 1isConnected[i][j] == isConnected[j][i]
代码
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
def dfs(i):
for j in range(n):
if isConnected[i][j] == 1 and j not in visited:
visited.add(j)
dfs(j)
visited = set()
circle = 0
n = len(isConnected)
for i in range(n):
if i not in visited:
dfs(i)
circle += 1
return circle
题目
1.6
cv的,没空复习并查集了
题目
399. 除法求值
难度中等293
给你一个变量对数组
equations和一个实数值数组values作为已知条件,其中equations[i] = [Ai, Bi]和values[i]共同表示等式Ai / Bi = values[i]。每个Ai或Bi是一个表示单个变量的字符串。另有一些以数组
queries表示的问题,其中queries[j] = [Cj, Dj]表示第j个问题,请你根据已知条件找出Cj / Dj = ?的结果作为答案。返回 所有问题的答案 。如果存在某个无法确定的答案,则用
-1.0替代这个答案。**注意:**输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]] 输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000] 解释: 条件:a / b = 2.0, b / c = 3.0 问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? 结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]] 输出:[3.75000,0.40000,5.00000,0.20000]示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]] 输出:[0.50000,2.00000,-1.00000,-1.00000]提示:
1 <= equations.length <= 20equations[i].length == 21 <= Ai.length, Bi.length <= 5values.length == equations.length0.0 < values[i] <= 20.01 <= queries.length <= 20queries[i].length == 21 <= Cj.length, Dj.length <= 5Ai, Bi, Cj, Dj由小写英文字母与数字组成
代码
class Solution:
def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
# 构造图,equations的第一项除以第二项等于value里的对应值,第二项除以第一项等于其倒数
graph = {}
for (x, y), v in zip(equations, values):
if x in graph:
graph[x][y] = v
else:
graph[x] = {y: v}
if y in graph:
graph[y][x] = 1/v
else:
graph[y] = {x: 1/v}
# dfs找寻从s到t的路径并返回结果叠乘后的边权重即结果
def dfs(s, t) -> int:
if s not in graph:
return -1
if t == s:
return 1
for node in graph[s].keys():
if node == t:
return graph[s][node]
elif node not in visited:
visited.add(node) # 添加到已访问避免重复遍历
v = dfs(node, t)
if v != -1:
return graph[s][node]*v
return -1
# 逐个计算query的值
res = []
for qs, qt in queries:
visited = set()
res.append(dfs(qs, qt))
return res
1.5
学校的课堂知识明明以后都用不上,却还是要为了绩点去复习
能直接快进到寒假不,我想快点开始学 JS 了
题目
830. 较大分组的位置
难度简单
在一个由小写字母构成的字符串
s中,包含由一些连续的相同字符所构成的分组。例如,在字符串
s = "abbxxxxzyy"中,就含有"a","bb","xxxx","z"和"yy"这样的一些分组。分组可以用区间
[start, end]表示,其中start和end分别表示该分组的起始和终止位置的下标。上例中的"xxxx"分组用区间表示为[3,6]。我们称所有包含大于或等于三个连续字符的分组为 较大分组 。
找到每一个 较大分组 的区间,按起始位置下标递增顺序排序后,返回结果。
示例 1:
输入:s = "abbxxxxzzy" 输出:[[3,6]] 解释:"xxxx" 是一个起始于 3 且终止于 6 的较大分组。示例 2:
输入:s = "abc" 输出:[] 解释:"a","b" 和 "c" 均不是符合要求的较大分组。示例 3:
输入:s = "abcdddeeeeaabbbcd" 输出:[[3,5],[6,9],[12,14]] 解释:较大分组为 "ddd", "eeee" 和 "bbb"示例 4:
输入:s = "aba" 输出:[]提示:
1 <= s.length <= 1000s仅含小写英文字母
代码
class Solution:
def largeGroupPositions(self, s: str) -> List[List[int]]:
last, cnt = "", 0
res = []
for i, word in enumerate(s):
if word == last:
cnt += 1
else:
if cnt>=3:
res.append([i-cnt,i-1])
cnt = 1
last = word
if cnt>=3:
res.append([len(s)-cnt,len(s)-1])
return res
1.4
考试周开始了 🙌
题目
509. 斐波那契数
难度简单
斐波那契数,通常用
F(n)表示,形成的序列称为 斐波那契数列 。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1给你
n,请计算F(n)。
代码
class Solution:
def fib(self, N: int) -> int:
dp = [0,1]
for i in range(1,N):
dp.append(dp[-1]+dp[-2])
return dp[N]
1.3
还挺简单的,俺复习去了
题目
86. 分隔链表
难度中等
给你一个链表和一个特定值
x,请你对链表进行分隔,使得所有小于x的节点都出现在大于或等于x的节点之前。你应当保留两个分区中每个节点的初始相对位置。
示例:
输入:head = 1->4->3->2->5->2, x = 3 输出:1->2->2->4->3->5
代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def partition(self, head: ListNode, x: int) -> ListNode:
node = head
dummy_small, dummy_large = ListNode(0), ListNode(0)
node_small, node_large = dummy_small, dummy_large
while node:
nxt_node = node.next
if node.val<x:
if node_small==dummy_small:
node_small = node
dummy_small.next = node_small
else:
node_small.next = node
node_small = node
node_small.next = None
else:
if node_large == dummy_large:
node_large = node
dummy_large.next = node_large
else:
node_large.next = node
node_large = node
node_large.next = None
node = nxt_node
node_small.next = dummy_large.next
return dummy_small.next
1.2
好家伙,昨天做完题直接忘记写了
题目
239. 滑动窗口最大值
难度困难
给你一个整数数组
nums,有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7示例 2:
输入:nums = [1], k = 1 输出:[1]示例 3:
输入:nums = [1,-1], k = 1 输出:[1,-1]示例 4:
输入:nums = [9,11], k = 2 输出:[11]示例 5:
输入:nums = [4,-2], k = 2 输出:[4]提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
代码
堆栈:时间复杂度O(NlogN)
import heapq
class Solution:
def maxSlidingWindow(self, nums, k):
heap = [(-nums[i], i) for i in range(k)]
heapq.heapify(heap)
res = [-heap[0][0]]
for i in range(k,len(nums)):
heapq.heappush(heap, (-nums[i], i))
while heap[0][1] <= i - k:
heapq.heappop(heap)
res.append(-heap[0][0])
return res
双向队列:时间复杂度O(N)
from collections import deque
class Solution:
def maxSlidingWindow(self, nums, k):
n = len(nums)
q = deque()
for i in range(k):
while q and nums[i] >= nums[q[-1]]:
q.pop()
q.append(i)
res = [nums[q[0]]]
for i in range(k, n):
while q and nums[i] >= nums[q[-1]]:
q.pop()
q.append(i)
while q[0] <= i - k:
q.popleft()
res.append(nums[q[0]])
return res
1.1
因为太简单而忘记更新 😓
题目
605. 种花问题
难度简单
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组
flowerbed表示花坛,由若干0和1组成,其中0表示没种植花,1表示种植了花。另有一个数n,能否在不打破种植规则的情况下种入n朵花?能则返回true,不能则返回false。示例 1:
输入:flowerbed = [1,0,0,0,1], n = 1 输出:true示例 2:
输入:flowerbed = [1,0,0,0,1], n = 2 输出:false提示:
1 <= flowerbed.length <= 2 * 104flowerbed[i]为0或1flowerbed中不存在相邻的两朵花0 <= n <= flowerbed.length
代码
class Solution:
def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:
cnt = 0
index = 0
size = len(flowerbed)
while index<size:
if flowerbed[index] == 1:
# 该位置有花
index += 2
elif index+1<size and flowerbed[index+1] == 1:
# 后一个位置有花
index += 3
elif index-1>=0 and flowerbed[index-1] == 1:
# 前一个位置有花
index += 1
else:
# 前中后均无花
flowerbed[index] = 1
cnt += 1
index += 2
return cnt>=n