2021年3月刷题日志
3.31
还没等到 MS 的正式 offer 🤦♂️
题目
90. 子集 II
难度中等
给你一个整数数组
nums,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]示例 2:
输入:nums = [0] 输出:[[],[0]]提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10
思路
迭代法
- 新建一个空数组
res,用于存放遍历到的所有子集,同时需要往数组中首先加一个空数组,代表空集 - 逐个遍历数组中的所有数,针对每个数字而言有两种情况
- 加入这个数
- 不加入这个数
- 对于上一次遍历所获得所有集合,都需要实行这两个操作
- 一般来说,假设原数组长度为
n第一次res会变成长度1 + 1,第二次会变成1 + 4… - 但是题目中的
nums中可能出现重复整数,所以需要想办法规避掉重复的子集的添加
重复子集判断
-
首先需要对数组
nums进行排序,保证是按顺序遍历的数字 -
我们在每次遍历的时候维护一个数组
last,用于记录当前res中的每个子集在上一次遍历的时候加入的数字 -
例如针对
[1, 2, 2]而言- 第一遍:
res = [[], [1]], last = [1, -11] - 第二遍:
res = [[], [1], [2], [1,2]], last = [2, 2, -11, -11] - 第三遍:
res = [[], [1], [2], [1,2], [2,2], [1,2,2]], last = [2, 2, 2, 2, -11, -11]
- 第一遍:
-
由于数字的范围是
[-10, 10],所以这里我用-11来表示该子集在上次遍历的时候没有新加入数字
代码
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsetsWithDup = function(nums) {
nums.sort()
let res = [[]]
let last = [-11]
for(let i = 0; i < nums.length; i++) {
// 每次有加入数字/不加入数字两个选项
const tmp = []
const nxt = []
for(let j = 0; j < res.length; j++){
tmp.push(res[j])
nxt.push(nums[i])
if(nums[i] != last[j]) {
tmp.push([...res[j],nums[i]])
nxt.push(-11)
}
}
res = tmp
last = nxt
}
return res
};
3.30
昨日事多,刷题没写日志
题目
74. 搜索二维矩阵
难度中等352
编写一个高效的算法来判断
m x n矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
示例 1:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true示例 2:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
思路
两周之前刷过的一道题,写两种思路
- 一维的二分
- 先根据第一列数字确定
target可能出现的行 - 再到对应行,利用
index(本质是二分),寻找target
- 先根据第一列数字确定
- 二维的二分
- 可以把二维数组的每行抽出来拼到一起,抽象出来之后对这个二维数组本身直接二分搜索即可
代码
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
# 二维二分
m, n = len(matrix), len(matrix[0])
left, right = 0, m * n - 1
while left <= right:
mid = (left + right) // 2
row, col = mid // n, mid % n
if matrix[row][col] < target:
left = mid + 1
elif matrix[row][col] > target:
right = mid - 1
else:
return True
return False
3.28
题目
173. 二叉搜索树迭代器
难度中等
实现一个二叉搜索树迭代器类
BSTIterator,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点root会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext()如果向指针右侧遍历存在数字,则返回true;否则返回false。int next()将指针向右移动,然后返回指针处的数字。注意,指针初始化为一个不存在于 BST 中的数字,所以对
next()的首次调用将返回 BST 中的最小元素。你可以假设
next()调用总是有效的,也就是说,当调用next()时,BST 的中序遍历中至少存在一个下一个数字。示例:
输入 ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] 输出 [null, 3, 7, true, 9, true, 15, true, 20, false] 解释 BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); bSTIterator.next(); // 返回 3 bSTIterator.next(); // 返回 7 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 9 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 15 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 20 bSTIterator.hasNext(); // 返回 False提示:
树中节点的数目在范围
[1, 105]内
0 <= Node.val <= 106最多调用
105次hasNext和next操作进阶:
- 你可以设计一个满足下述条件的解决方案吗?
next()和hasNext()操作均摊时间复杂度为O(1),并使用O(h)内存。其中h是树的高度。
思路
迭代,利用栈模拟递归
代码
/**
* @param {TreeNode} root
*/
var BSTIterator = function(root) {
this.stk = []
this.cur = root
};
/**
* @return {number}
*/
BSTIterator.prototype.next = function() {
while (this.cur) {
this.stk.push(this.cur)
this.cur = this.cur.left
}
this.cur = this.stk.pop()
const res = this.cur.val
this.cur = this.cur.right
return res
};
/**
* @return {boolean}
*/
BSTIterator.prototype.hasNext = function() {
return this.stk.length > 0 || this.cur !== null
};
3.27
美好的周六,哦哈哟
题目
61. 旋转链表
难度中等
给你一个链表的头节点
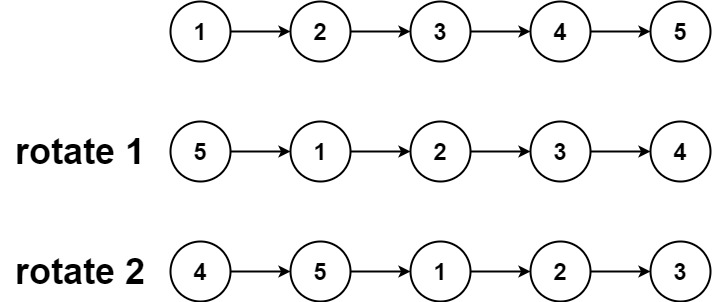
head,旋转链表,将链表每个节点向右移动k个位置。示例 1:
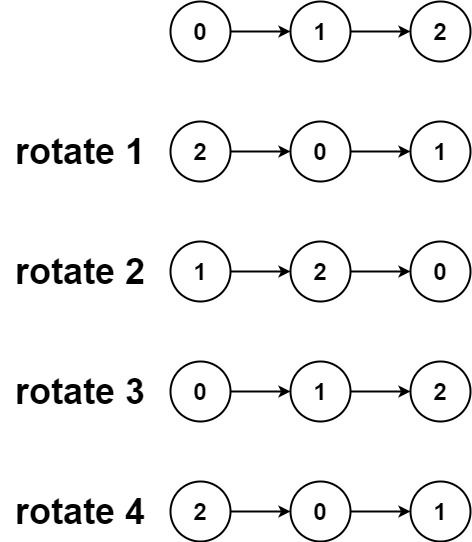
输入:head = [1,2,3,4,5], k = 2 输出:[4,5,1,2,3]示例 2:
输入:head = [0,1,2], k = 4 输出:[2,0,1]提示:
- 链表中节点的数目在范围
[0, 500]内-100 <= Node.val <= 1000 <= k <= 2 * 10^9
思路
经典快慢指针,和之前一道好像叫翻转链表的题目差不多,思路也几乎一样。区别是之前那道题的 k 是比链表小的,所以快指针不会超过尾结点。
- 快慢指针指向头结点
- 先将快指针往后移动
k个位置- 由于题目说明
k <= 2*10^9,所以直接往后移动k个位置是很浪费时间的 - 考虑到结点数目小于 500,于是在第一次向后移动的时候,我们会记录下链表的长度
- 当快指针指向尾结点的时候,通过链表长度和
k,我们可以直接计算出还应该往后移动多少个单位
- 由于题目说明
- 当快指针在合适的位置之后,令快慢指针同时向后移,直到快指针指向尾结点
- 这个时候把慢指针后面的那段链表拼接到头节点前面即可
代码
var rotateRight = function(head, k) {
if (! head) {
return head
}
const dummy = new ListNode(0, head)
let fast = head
let slow = head
let cnt = 1
// 先将快指针往后移动k个
while (k>0) {
if (fast.next) {
fast = fast.next
cnt += 1
k -= 1
}
else {
fast = head
k -= 1
k %= cnt
}
}
// 两根指针同时往后移,直到快指针指向尾结点
while(fast.next) {
fast = fast.next
slow = slow.next
}
// 将慢指针后面的链表迁移到原头节点前
fast.next = dummy.next
dummy.next = slow.next
slow.next = null
return dummy.next
};
3.26
昨天每日一题的简化版。
题目
83. 删除排序链表中的重复元素
难度简单
存在一个按升序排列的链表,给你这个链表的头节点
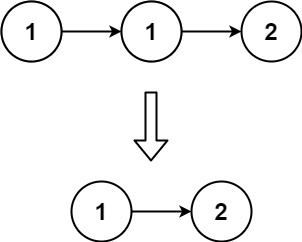
head,请你删除所有重复的元素,使每个元素 只出现一次 。返回同样按升序排列的结果链表。
示例 1:
输入:head = [1,1,2] 输出:[1,2]示例 2:
输入:head = [1,1,2,3,3] 输出:[1,2,3]提示:
- 链表中节点数目在范围
[0, 300]内-100 <= Node.val <= 100- 题目数据保证链表已经按升序排列
代码
var deleteDuplicates = function(head) {
const dummy = new ListNode(101, head)
let node = dummy
while(node.next) {
if(node.next.val == node.val) {
node.next = node.next.next
} else {
node = node.next
}
}
return dummy.next
};
3.25
题目
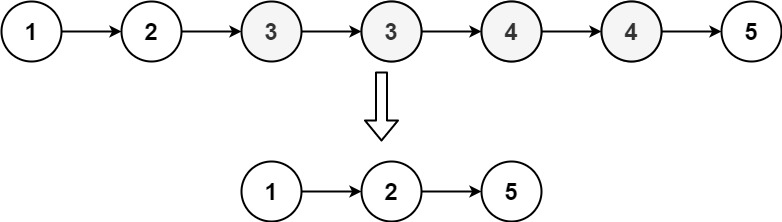
82. 删除排序链表中的重复元素 II
难度中等
存在一个按升序排列的链表,给你这个链表的头节点
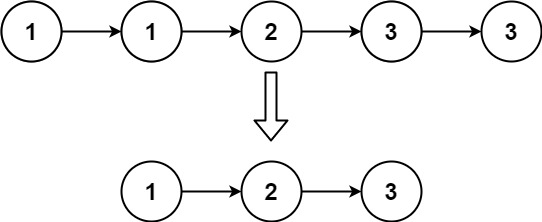
head,请你删除链表中所有存在数字重复情况的节点,只保留原始链表中 没有重复出现 的数字。返回同样按升序排列的结果链表。
示例 1:
输入:head = [1,2,3,3,4,4,5] 输出:[1,2,5]示例 2:
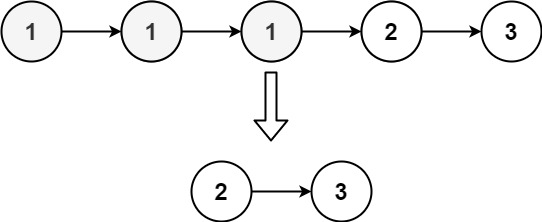
输入:head = [1,1,1,2,3] 输出:[2,3]提示:
- 链表中节点数目在范围
[0, 300]内-100 <= Node.val <= 100- 题目数据保证链表已经按升序排列
思路
一次遍历
设置一个哑节点 dummy 放到 head 的前面,从 dummy 开始向后遍历。
当遇到后一个结点的值和后一个的后一个的结点的值一样的时候,就记录下后一个结点的值 x,然后把之后所有值为 x 的结点全部去掉。
代码
var deleteDuplicates = function(head) {
const dummy = new ListNode(0)
dummy.next = head
let node = dummy
while(node.next && node.next.next) {
if(node.next.val == node.next.next.val) {
let x = node.next.val
while (node.next && node.next.val == x) {
node.next = node.next.next
}
} else {
node = node.next
}
}
return dummy.next
};
3.24
题目
456. 132模式
难度中等363
给你一个整数数组
nums,数组中共有n个整数。132 模式的子序列 由三个整数nums[i]、nums[j]和nums[k]组成,并同时满足:i < j < k和nums[i] < nums[k] < nums[j]。如果
nums中存在 132 模式的子序列 ,返回true;否则,返回false。**进阶:**很容易想到时间复杂度为
O(n^2)的解决方案,你可以设计一个时间复杂度为O(n logn)或O(n)的解决方案吗?示例 1:
输入:nums = [1,2,3,4] 输出:false 解释:序列中不存在 132 模式的子序列。示例 2:
输入:nums = [3,1,4,2] 输出:true 解释:序列中有 1 个 132 模式的子序列: [1, 4, 2] 。示例 3:
输入:nums = [-1,3,2,0] 输出:true 解释:序列中有 3 个 132 模式的的子序列:[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。提示:
n == nums.length1 <= n <= 104-109 <= nums[i] <= 109
代码
class Solution:
def find132pattern(self, nums: List[int]) -> bool:
n = len(nums)
left_min = [0] * n
cur = nums[0]
for i in range(n):
cur = min(cur, nums[i])
left_min[i] = cur
stk = []
for j in range(n-1, -1, -1):
while stk and stk[-1] <= left_min[j]:
stk.pop()
if stk and stk[-1] < nums[j]:
return True
stk.append(nums[j])
return False
3.22
题目
341. 扁平化嵌套列表迭代器
难度中等
给你一个嵌套的整型列表。请你设计一个迭代器,使其能够遍历这个整型列表中的所有整数。
列表中的每一项或者为一个整数,或者是另一个列表。其中列表的元素也可能是整数或是其他列表。
示例 1:
输入: [[1,1],2,[1,1]] 输出: [1,1,2,1,1] 解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,1,2,1,1]。示例 2:
输入: [1,[4,[6]]] 输出: [1,4,6] 解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,4,6]。
思路
- 递归:在初始化函数中就利用深搜把数组处理成扁平的
- 迭代:在
hasNext方法中用栈模拟递归,每次把栈顶元素转换成数字之后再返回True
代码
递归
class NestedIterator:
def __init__(self, nestedList: [NestedInteger]):
nums = []
def dfs(nestedList):
for nest in nestedList:
if nest.isInteger():
nums.append(nest.getInteger())
else:
dfs(nest.getList())
dfs(nestedList)
self.val = nums[::-1]
def next(self) -> int:
return self.val.pop()
def hasNext(self) -> bool:
if len(self.val):
return True
return False
迭代
class NestedIterator:
def __init__(self, nestedList: [NestedInteger]):
self.stk = nestedList
def next(self) -> int:
return self.stk.pop(0).getInteger()
def hasNext(self) -> bool:
while self.stk:
if self.stk[0].isInteger():
return True
else:
nest = self.stk.pop(0)
self.stk = nest.getList() + self.stk
3.21
题目
73. 矩阵置零
难度中等428
给定一个
*m* x *n*的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**进阶:
一个直观的解决方案是使用
O(*m**n*)的额外空间,但这并不是一个好的解决方案。一个简单的改进方案是使用
O(*m* + *n*)的额外空间,但这仍然不是最好的解决方案。你能想出一个仅使用常量空间的解决方案吗?
示例 1:
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2:
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
思路
跟着题目中的进阶方案思路去思考
- 一个直观的解决方案是使用
O(m*n)的额外空间,但这并不是一个好的解决方案。
直接克隆原矩阵,然后遍历原矩阵,如果遇到 0 就将新矩阵中的对应行和列置 0。
- 一个简单的改进方案是使用
O(m + n)的额外空间,但这仍然不是最好的解决方案。
新建两个数组 rows, cols,遍历一遍原矩阵存储需要被置 0 的行和列,然后根据这两个数组对行和列进行置 0。
- 你能想出一个仅使用常量空间的解决方案吗?
看了题解,真是鬼才。用第一行和第一列的来作为我们刚刚设置的两个数组,标记需要被置 0 的行和列。不过需要另外设置两个变量来记录第一行和第一列中有没有原生的0。
题解中给出了只需要一个变量的解法,思路是
3.20
昨天的题目太降智了,没记下来。
题目
150. 逆波兰表达式求值
难度中等
根据 逆波兰表示法,求表达式的值。
有效的算符包括
+、-、*、/。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释: 该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22提示:
1 <= tokens.length <= 104tokens[i]要么是一个算符("+"、"-"、"*"或"/"),要么是一个在范围[-200, 200]内的整数
思路
Leetcode 直接把解题方法写在了问题的后面。
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中。
我们直接跟着他的指示,用栈这么做就行了。记得上次遇到这个逆波兰表达式还是在大二上学期的数据结构课上,当时老师会让我们手动转成逆波兰和波兰表达式。
代码
/**
* @param {string[]} tokens
* @return {number}
*/
var evalRPN = function(tokens) {
const nums = new Array()
const n = tokens.length
for (let i = 0; i < n; i++) {
const token = tokens[i]
if (isNumber(token)) {
nums.push(Number(token))
} else {
const num2 = nums.pop()
const num1 = nums.pop()
let res = 0
if (token == '+') {
res = num1 + num2
} else if(token == '-') {
res = num1 - num2
} else if (token == '*') {
res = num1 * num2
} else if (token == '/') {
res = parseInt(num1 / num2)
}
nums.push(res)
}
}
return nums[0]
};
const isNumber = (token) => {
return !(token == '+' || token == '-' || token == '*' || token == '/')
}
3.18
题目
115. 不同的子序列
难度困难
给定一个字符串
s和一个字符串t,计算在s的子序列中t出现的个数。字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,
"ACE"是"ABCDE"的一个子序列,而"AEC"不是)题目数据保证答案符合 32 位带符号整数范围。
示例 1:
输入:s = "rabbbit", t = "rabbit" 输出:3 解释: 如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。 (上箭头符号 ^ 表示选取的字母) rabbbit ^^^^ ^^ rabbbit ^^ ^^^^ rabbbit ^^^ ^^^示例 2:
输入:s = "babgbag", t = "bag" 输出:5 解释: 如下图所示, 有 5 种可以从 s 中得到 "bag" 的方案。 (上箭头符号 ^ 表示选取的字母) babgbag ^^ ^ babgbag ^^ ^ babgbag ^ ^^ babgbag ^ ^^ babgbag ^^^提示:
0 <= s.length, t.length <= 1000s和t由英文字母组成
思路
动态规划,设字符串 s 长度为 m,t 长度为 n
- DP table:
m+1行,n+1列,初始化为0,dp[i][j]代表的是s[i:]中子序列t[j:]的个数。 - Base case:最后一列,即
j = n的时候,目标子序列为空串,则子串数应该为1;最后一行,即当i = m的时候,无论目标子序列为何,自身都是空串,所以子串数为0。 - 状态转移方程:考虑
dp[i][j]的大小的时候,应该分两种递推的情况s[i] == t[j],此时当前的子序列是可以直接从各字符串的后一个位置递推过来dp[i][j] += dp[i+1][j+1],当然也可以从当前字符串的后一个位置递推过来dp[i][j] += dp[i+1][j]s[i] != t[j],这个时候就必不能匹配当前位置,则只能dp[i][j] += dp[i+1][j]
代码
class Solution:
def numDistinct(self, s: str, t: str) -> int:
m, n= len(s), len(t)
dp = [[0] * (n + 1) for _ in range(m + 1)]
# dp[i][j] 代表的意思是 s[i:] 和 t[j:] 的子序列数
for i in range(m+1):
# 最后一列初始化为 1
dp[i][n] = 1
for i in range(n):
# 最后一行初始化为 0
dp[m][i] = 0
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
if s[i] == t[j]:
dp[i][j] = dp[i+1][j+1] + dp[i+1][j]
else:
dp[i][j] = dp[i+1][j]
return dp[0][0]
3.17
题目
118. 杨辉三角
难度简单
给定一个非负整数
numRows,生成杨辉三角的前numRows行。
代码
/**
* @param {number} numRows
* @return {number[][]}
*/
var generate = function(numRows) {
const res = []
for (let i = 0; i < numRows; i++) {
const arr = new Array(i+1).fill(1);
for(let j = 1; j < i; j++){
arr[j] = res[i-1][j-1] + res[i-1][j]
}
res.push(arr)
}
return res
};
3.15
久违的原题
题目
54. 螺旋矩阵
难度中等
给你一个
m行n列的矩阵matrix,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
思路
- 模拟螺旋:想象成有一个小人从左上角出发,他的方向顺序分别是:
[右,下,左,上],当即将撞到墙或者走上回头路的时候,小人都会非常机智地调整方向。 - 按圈迭代:将整个迷宫看成由若干个矩形边框组成,这个边框由最外层往最里层,逐渐缩小。每次只需要确定一个左上角,一个右下角,就可以很方便地遍历整个方框。我们依次迭代左上角和右下角的位置,直到两个点重合。
代码
模拟螺旋
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
# 右 下 左 上
directions = [[0, 1], [1, 0], [0, -1], [-1, 0]]
m, n = len(matrix), len(matrix[0])
visited = [[0]* n for _ in range(m)]
i, j, k = 0, 0, 0
res = []
res.append(matrix[0][0])
visited[0][0] = 1
x, y = 0, 1
for _ in range(m*n-1):
while not (0 <= i + x < m) or not(0 <= j + y < n) or visited[i+x][j+y]:
k = (k + 1) % 4
x, y = directions[k]
i += x
j += y
res.append(matrix[i][j])
visited[i][j] = 1
return res
按圈迭代
/**
* @param {number[][]} matrix
* @return {number[]}
*/
var spiralOrder = function(matrix) {
const res = new Array();
const m = matrix.length;
const n = matrix[0].length;
let left = 0, right = n - 1, bottom = 0, top = m - 1
while (left <= right && bottom <= top){
for (let i = left; i <= right; i++) res.push(matrix[bottom][i]);
for (let i = bottom + 1; i <= top; i++) res.push(matrix[i][right])
if (left < right && bottom < top) {
for (let i = right - 1; i > left; i--) res.push(matrix[top][i]);
for (let i = top ; i > bottom; i--) res.push(matrix[i][left]);
}
[left, right, bottom, top] = [left + 1, right - 1, bottom + 1, top - 1]
}
return res;
};
3.14
题目
706. 设计哈希映射
难度简单
不使用任何内建的哈希表库设计一个哈希映射(HashMap)。
实现
MyHashMap类:
MyHashMap()用空映射初始化对象
void put(int key, int value)向 HashMap 插入一个键值对(key, value)。如果key已经存在于映射中,则更新其对应的值value。
int get(int key)返回特定的key所映射的value;如果映射中不包含key的映射,返回-1。
void remove(key)如果映射中存在key的映射,则移除key和它所对应的value。示例:
输入: ["MyHashMap", "put", "put", "get", "get", "put", "get", "remove", "get"] [[], [1, 1], [2, 2], [1], [3], [2, 1], [2], [2], [2]] 输出: [null, null, null, 1, -1, null, 1, null, -1] 解释: MyHashMap myHashMap = new MyHashMap(); myHashMap.put(1, 1); // myHashMap 现在为 [[1,1]] myHashMap.put(2, 2); // myHashMap 现在为 [[1,1], [2,2]] myHashMap.get(1); // 返回 1 ,myHashMap 现在为 [[1,1], [2,2]] myHashMap.get(3); // 返回 -1(未找到),myHashMap 现在为 [[1,1], [2,2]] myHashMap.put(2, 1); // myHashMap 现在为 [[1,1], [2,1]](更新已有的值) myHashMap.get(2); // 返回 1 ,myHashMap 现在为 [[1,1], [2,1]] myHashMap.remove(2); // 删除键为 2 的数据,myHashMap 现在为 [[1,1]] myHashMap.get(2); // 返回 -1(未找到),myHashMap 现在为 [[1,1]]提示:
0 <= key, value <= 106- 最多调用
104次put、get和remove方法
思路
和昨天代码相差无几,昨天是直接存 value,今天是存键值对 [key, value]
代码
/**
* Initialize your data structure here.
*/
var MyHashMap = function() {
this.BASE = 769;
this.arr = new Array(this.BASE).fill(0).map(() => new Array());
};
MyHashMap.prototype.hash = function(key) {
return key % this.BASE;
}
/**
* value will always be non-negative.
* @param {number} key
* @param {number} value
* @return {void}
*/
MyHashMap.prototype.put = function(key, value) {
const h = this.hash(key);
for (const subArr of this.arr[h]) {
if (subArr[0] == key) {
subArr[1] = value;
return;
}
}
this.arr[h].push([key, value]);
};
/**
* Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key
* @param {number} key
* @return {number}
*/
MyHashMap.prototype.get = function(key) {
const h = this.hash(key);
for (const subArr of this.arr[h]){
if (subArr[0] == key) {
return subArr[1];
}
}
return -1;
};
/**
* Removes the mapping of the specified value key if this map contains a mapping for the key
* @param {number} key
* @return {void}
*/
MyHashMap.prototype.remove = function(key) {
const h = this.hash(key);
const subs = this.arr[h];
for (let i = 0; i < subs.length; i++){
if(subs[i][0] == key) {
subs.splice(i, 1);
}
}
};
/**
* Your MyHashMap object will be instantiated and called as such:
* var obj = new MyHashMap()
* obj.put(key,value)
* var param_2 = obj.get(key)
* obj.remove(key)
*/
3.13
题目
705. 设计哈希集合
难度简单
不使用任何内建的哈希表库设计一个哈希集合(HashSet)。
实现
MyHashSet类:
void add(key)向哈希集合中插入值key。bool contains(key)返回哈希集合中是否存在这个值key。void remove(key)将给定值key从哈希集合中删除。如果哈希集合中没有这个值,什么也不做。示例:
输入: ["MyHashSet", "add", "add", "contains", "contains", "add", "contains", "remove", "contains"] [[], [1], [2], [1], [3], [2], [2], [2], [2]] 输出: [null, null, null, true, false, null, true, null, false] 解释: MyHashSet myHashSet = new MyHashSet(); myHashSet.add(1); // set = [1] myHashSet.add(2); // set = [1, 2] myHashSet.contains(1); // 返回 True myHashSet.contains(3); // 返回 False ,(未找到) myHashSet.add(2); // set = [1, 2] myHashSet.contains(2); // 返回 True myHashSet.remove(2); // set = [1] myHashSet.contains(2); // 返回 False ,(已移除)提示:
0 <= key <= 10^6最多调用
104次add、remove和contains。**进阶:**你可以不使用内建的哈希集合库解决此问题吗?
思路
无脑法:开辟一个长度为 10^6 + 1 的数组,然后把出现的数字 num 放到 index = num 的位置上去,也就是不做哈希映射。
有脑法:去一个质数,把出现的数字 num 放到 index = num mod 769 的一个链表上去。
代码
无脑
class MyHashSet:
def __init__(self):
"""
Initialize your data structure here.
"""
self.cnts = [0] * 1000001
def add(self, key: int) -> None:
self.cnts[key] = 1
def remove(self, key: int) -> None:
if self.cnts[key]:
self.cnts[key] -= 1
def contains(self, key: int) -> bool:
"""
Returns true if this set contains the specified element
"""
if self.cnts[key] > 0:
return True
else:
return False
有脑
/**
* Initialize your data structure here.
*/
var MyHashSet = function() {
this.BASE = 769;
this.data = new Array(this.BASE).fill(0).map(() => new Array());
};
/**
* @param {number} key
* @return {void}
*/
MyHashSet.prototype.add = function(key) {
const h = this.hash(key);
for (const element of this.data[h]) {
if (element == key) {
return
}
}
this.data[h].push(key);
};
/**
* @param {number} key
* @return {void}
*/
MyHashSet.prototype.remove = function(key) {
const h = this.hash(key);
const d = this.data[h];
for (let i = 0; i < d.length; i++) {
if (d[i] == key) {
d.splice(i, 1)
return
}
}
};
/**
* Returns true if this set contains the specified element
* @param {number} key
* @return {boolean}
*/
MyHashSet.prototype.contains = function(key) {
const h = this.hash(key);
const d = this.data[h];
for (let i = 0; i < d.length; i++) {
if (d[i] == key) {
return true
}
}
return false
};
MyHashSet.prototype.hash = function(key) {
return key % this.BASE;
}
3.12
昨天又收到面试📞,next Wed MS 二面
题目
331. 验证二叉树的前序序列化
难度中等
序列化二叉树的一种方法是使用前序遍历。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如
#。_9_ / \ 3 2 / \ / \ 4 1 # 6 / \ / \ / \ # # # # # #例如,上面的二叉树可以被序列化为字符串
"9,3,4,#,#,1,#,#,2,#,6,#,#",其中#代表一个空节点。给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
每个以逗号分隔的字符或为一个整数或为一个表示
null指针的'#'。你可以认为输入格式总是有效的,例如它永远不会包含两个连续的逗号,比如
"1,,3"。示例 1:
输入: "9,3,4,#,#,1,#,#,2,#,6,#,#" 输出: true示例 2:
输入: "1,#" 输出: false示例 3:
输入: "9,#,#,1" 输出: false
思路
官方题解,这个方法针不戳,偷一张图过来。
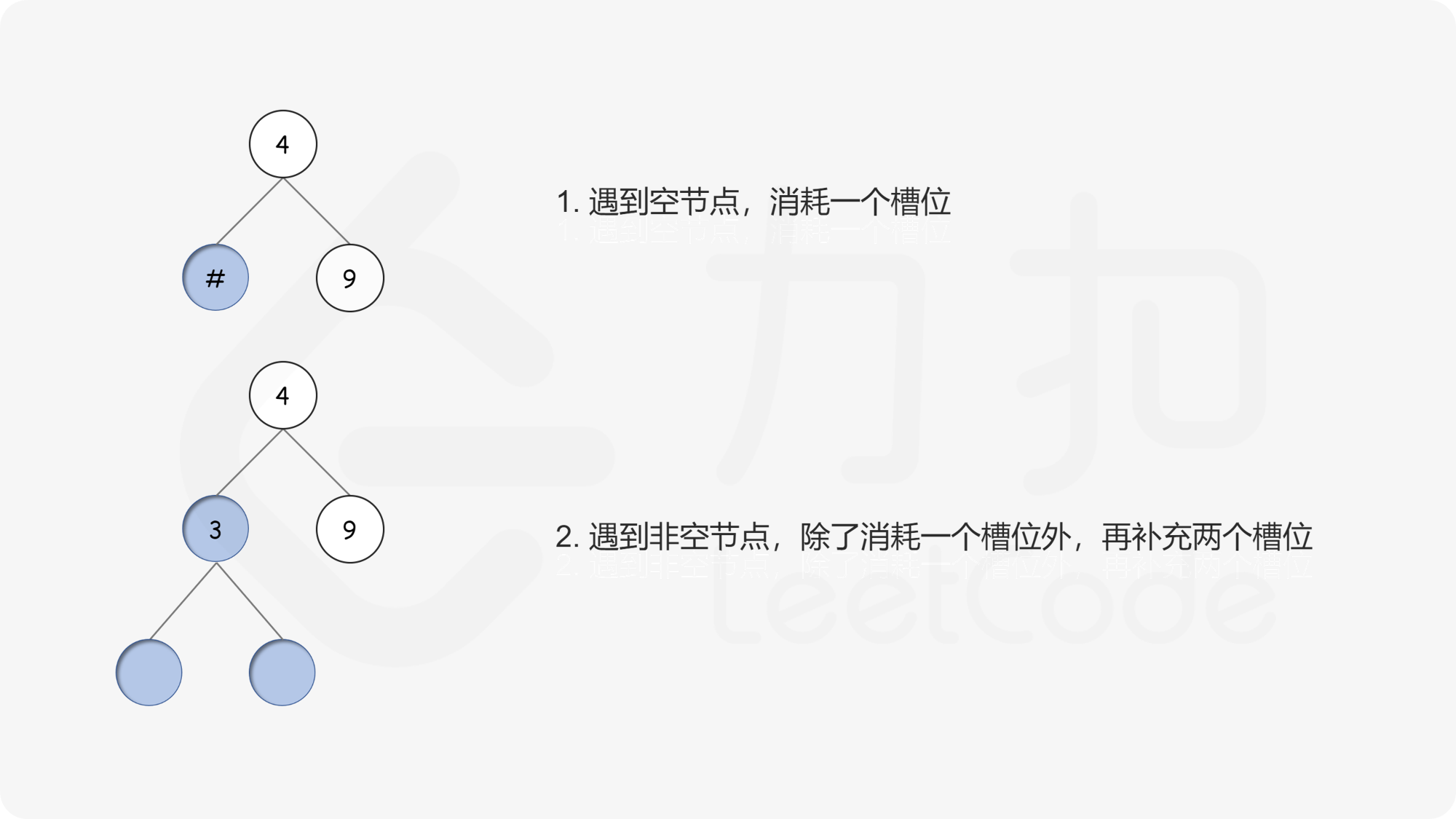
根据这个思路,我们只需要
- 将初始槽位设为
1,可以理解为需要一个槽位放根节点,同时#也是合法的空树。 - 遍历一遍结点数组,遇到非空结点就
++,遇到空结点就-- - 如果遍历中发现槽位数小于
0,说明就构不成树了 - 最后返回
槽位数 == 0
代码
class Solution:
def isValidSerialization(self, preorder: str) -> bool:
nodes = preorder.split(",")
cnt = 1
for i in nodes:
if cnt <= 0:
return False
if i == '#':
cnt -= 1
else:
cnt += 1
return cnt == 0
/**
* @param {string} preorder
* @return {boolean}
*/
var isValidSerialization = function(preorder) {
const nodes = preorder.split(",")
let cnt = 1;
for (let node of nodes) {
if (cnt <= 0) {
return false
}
if (node == '#') {
cnt -= 1
} else{
cnt += 1
}
}
return cnt == 0
};
3.11
MS 一面总算是过去了,马马虎虎吧,至少让我看到了或许对实习生的要求不会特别高
题目
227. 基本计算器 II
难度中等
给你一个字符串表达式
s,请你实现一个基本计算器来计算并返回它的值。整数除法仅保留整数部分。
示例 1:
输入:s = "3+2*2" 输出:7示例 2:
输入:s = " 3/2 " 输出:1示例 3:
输入:s = " 3+5 / 2 " 输出:5提示:
1 <= s.length <= 3 * 105s由整数和算符('+', '-', '*', '/')组成,中间由一些空格隔开s表示一个 有效表达式- 表达式中的所有整数都是非负整数,且在范围
[0, 231 - 1]内- 题目数据保证答案是一个 32-bit 整数
思路
用栈保存所有项,然后最后加起来,这里的项包括可以合并成一个数字的乘数法式子,比如 3 + 1 * 2 - 4,最后栈中应该就是三项 [3, 2, -4]。
遍历字符串,记录运算符和数字,并不断地压入栈,最后求栈的和即可。
代码
class Solution:
def calculate(self, s: str) -> int:
s = s.replace(" ", "") # 先去除字符串内的空格
s += "+" # 使得循环中能够处理最后一个项
n = len(s)
num = int()
nums = []
opt = "+"
for i in range(n):
ch = s[i]
if ch.isdigit():
num = num * 10 + int(ch)
else:
if opt == '+':
nums.append(num)
elif opt == '-':
nums.append(-num)
elif opt == '*':
nums.append(nums.pop() * num)
elif opt == '/':
nums.append(int(nums.pop() / num))
opt = s[i]
num = 0
return sum(nums)
3.10
昨天突然通知今天晚上 MS 实习面试,给爷紧张坏了。
题目
224. 基本计算器
难度困难
实现一个基本的计算器来计算一个简单的字符串表达式
s的值。示例 1:
输入:s = "1 + 1" 输出:2示例 2:
输入:s = " 2-1 + 2 " 输出:3示例 3:
输入:s = "(1+(4+5+2)-3)+(6+8)" 输出:23提示:
1 <= s.length <= 3 * 105s由数字、'+'、'-'、'('、')'、和' '组成s表示一个有效的表达式
思路
这道题因为没有乘法和除法,所以对于数值而言不需要用栈存储,只需要用栈存取运算符即可。
我们用 1 来代表 +,用 -1 代表 +,一开始默认为 1。
以 1-(3-4) 为例
opt = 1, num = 0, res = 0- 遍历到了
1,opt = 1, num = 1, res = 0 - 遍历到了
-,要对运算符进行取反,而且由于不是数字,所以对之前的结果进行计算,opt = -1, num = 0, res = 1 - 遍历到了
(,将之前的运算符压入栈(因为括号内的运算符不能影响外界),stk = [1, -1] - 遍历到了
3,暂存数字,num = 3 - 遍历到了
-,对栈顶运算符取反,由于栈顶原来是-1,所以现在的运算符变成了1,即加号;同时计算之前暂存的数字 - 遍历到了
4,暂存数字 - 遍历到了
),将栈顶的操作符压出,因为括号外要维持原运算符,计算暂存的数字
代码
class Solution:
def calculate(self, s: str) -> int:
stk = [1] # 存储标点符号的栈
s = s.replace(" ", "")
res ,num, opt =0, 0, 1 # 默认初始的标点符号为 +
for i in s:
if i.isdigit():
num = num * 10 + int(i)
else:
res += num * opt
num = 0
if i == '+':
opt = stk[-1]
elif i == '-':
opt = -stk[-1]
elif i == '(':
stk.append(opt)
elif i == ')':
stk.pop()
res += num * opt
return res
3.9
题目
1047. 删除字符串中的所有相邻重复项
难度简单
给出由小写字母组成的字符串
S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
输入:"abbaca" 输出:"ca" 解释: 例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。提示:
1 <= S.length <= 20000S仅由小写英文字母组成。
思路
一开始竟然朝着偶数长度的回文串这个思路去想了,属于前几天的后遗症吧,要抛弃这种思维定势。
其实就是很纯粹的用栈去判断是否要抛弃当前字母罢了。
代码
class Solution:
def removeDuplicates(self, S: str) -> str:
n = len(S)
stk = []
for i in S:
if not stk or stk[-1] != i:
stk.append(i)
else:
stk.pop()
return "".join(stk)
/**
* @param {string} S
* @return {string}
*/
var removeDuplicates = function(S) {
const stk = new Array();
for (const ch of S) {
if(stk.length == 0 || stk[stk.length - 1] != ch){
stk.push(ch);
} else {
stk.pop();
}
}
return stk.join("")
};
3.8
HAPPY WOMENS DAY
题目
132. 分割回文串 II
难度困难
给你一个字符串
s,请你将s分割成一些子串,使每个子串都是回文。返回符合要求的 最少分割次数 。
示例 1:
输入:s = "aab" 输出:1 解释:只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。示例 2:
输入:s = "a" 输出:0示例 3:
输入:s = "ab" 输出:1提示:
1 <= s.length <= 2000s仅由小写英文字母组成
思路
两次 DP
-
第一次 DP 求出任意子串是否为回文串。
-
第二次 DP 求出最少需要分割多少次。
代码
class Solution:
def minCut(self, s: str) -> int:
n = len(s)
f = [[True]*n for _ in range(n)]
for i in range(n-1, -1, -1):
for j in range(i+1,n):
f[i][j] = f[i+1][j-1] and (s[i] == s[j])
dp = [float('inf')] * n
for i in range(n):
if f[0][i]:
dp[i] = 0
else:
for j in range(i):
if f[j+1][i]:
dp[i] = min(dp[i], dp[j] + 1)
return dp[n-1]
3.7
又是菜到中等题看题解的一天。
题目
131. 分割回文串
难度中等522
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]
思路
回溯(DFS)+ 动态规划
首先用动态规划的思想,求解出任意子串是否为回文串。
然后用 DFS 的方法,从头开始遍历字符串,在可能拆分成子串的时候进行递归。
代码
class Solution:
def partition(self, s: str) -> List[List[str]]:
n = len(s)
dp = [[True] * n for _ in range(n)]
for i in range(n-1, -1, -1):
for j in range(i+1,n):
dp[i][j] = dp[i+1][j-1] and (s[i] == s[j])
res, tmp = [], []
def dfs(i):
if i == n:
res.append(tmp[:])
return
for j in range(i, n):
if dp[i][j]:
tmp.append(s[i:j+1])
dfs(j+1)
tmp.pop()
dfs(0)
return res
3.6
回归校园,网易云 start!
题目
503. 下一个更大元素 II
难度中等
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
输入: [1,2,1] 输出: [2,-1,2] 解释: 第一个 1 的下一个更大的数是 2; 数字 2 找不到下一个更大的数; 第二个 1 的下一个最大的数需要循环搜索,结果也是 2。注意: 输入数组的长度不会超过 10000。
思路
单调栈 + 循环数组。
单调栈,顾名思义就是从栈底到栈顶是单调递增或者单调递减的栈。本题中我们要构造的栈应该是递增栈。
栈中存放的是各个元素的下表,可以说是暂时还没有找到下一个更大元素的元素下标。
例如,[1, 2, 1],一开始栈为 [],所以栈中应该放入下标 0,当遍历到第二个元素的时候,发现 2 > 1,所以这时候就找到了下标为 0 的元素的下一个更大元素,因此就把 0 压出栈,然后将下标 1 压入栈。
通过这个方法,还不能确保找到所有元素的下一个更大元素,例如 [3, 2, 1],光遍历一遍数组是不够的,需要遍历两边,因此会用到循环数组。
代码
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
n = len(nums)
stk, res = [], [-1 for _ in range(n)]
for i in range(n*2 - 1):
index = i % n
while stk and nums[stk[-1]] < nums[index]:
res[stk.pop()] = nums[index]
stk.append(index)
return res
3.5
easy!
题目
232. 用栈实现队列
难度简单
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列的支持的所有操作(
push、pop、peek、empty):实现
MyQueue类:
void push(int x)将元素 x 推到队列的末尾
int pop()从队列的开头移除并返回元素
int peek()返回队列开头的元素
boolean empty()如果队列为空,返回true;否则,返回false说明:
你只能使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
进阶:
你能否实现每个操作均摊时间复杂度为
O(1)的队列?换句话说,执行n个操作的总时间复杂度为O(n),即使其中一个操作可能花费较长时间。示例:
输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty- 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)
思路
双栈模拟队列,似乎之前做过一个双队列模拟栈的,所以很快想到了这个方法。
虽然两个都是栈,但是我们使用的时候,第二个栈的逻辑是按照队列的倒叙考虑的。
对于 push 操作,所有的元素放到 stk1 中。
对于 pop 操作,由于需要返回的是队首的元素,也就是第一个进栈的元素,因此需要把 stk1 中的所有元素依次压出并压入 stk2。这样就实现了一个倒序的队列。即 stk2 的栈顶是队首元素,队伍依次从栈顶排到栈底,这样子出队顺序就合理了。因此 pop 掉 stk2 的栈顶元素即可。
对于 peek 操作,同上。
对于 empty 操作,只需要判断当前两个队列是否均为空。
代码
class MyQueue:
def __init__(self):
"""
Initialize your data structure here.
"""
self.stk1 = []
self.stk2 = []
def push(self, x: int) -> None:
"""
Push element x to the back of queue.
"""
self.stk1.append(x)
def pop(self) -> int:
"""
Removes the element from in front of queue and returns that element.
"""
if not self.stk2:
while self.stk1:
self.stk2.append(self.stk1.pop())
return self.stk2.pop()
def peek(self) -> int:
"""
Get the front element.
"""
if not self.stk2:
while self.stk1:
self.stk2.append(self.stk1.pop())
return self.stk2[-1]
def empty(self) -> bool:
"""
Returns whether the queue is empty.
"""
return len(self.stk1)+len(self.stk2) == 0
# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()
3.4
题目
354. 俄罗斯套娃信封问题
难度困难
给定一些标记了宽度和高度的信封,宽度和高度以整数对形式
(w, h)出现。当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
说明: 不允许旋转信封。
示例:
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]] 输出: 3 解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
思路
把两个维度的问题分开考虑,我们首先按照宽度对信封进行升序排列,为了确保不会重复考虑一个宽度会算多个信封,需要对同样宽度的信封按降序排列。
为了尝试找到高度的最长递增序列,首先将第一封信的高度放到结果序列中,然后遍历剩下所有的信封高度。
算法流程:
- 如果当前的高度比结果序列中的最后一个高度还要高,就直接放到序列尾部
- 否则,就把当前的高度插入到序列的合适的位置中去,通过二分查找的方式,找到当前高度能够插入的位置。这个位置保证了插入后的序列仍然是递增序列,而且这个位置的数可能会变小。
代码
class Solution:
def maxEnvelopes(self, envelopes: List[List[int]]) -> int:
envelopes.sort(key = lambda x:(x[0], -x[1]))
if not envelopes: return 0
f = [envelopes[0][1]]
for i in range(1, len(envelopes)):
if (num := envelopes[i][1]) > f[-1]:
f.append(num)
else:
index = bisect.bisect_left(f, num) # 找到num可以插入的位置
f[index] = num
return len(f)
3.3
题目
338. 比特位计数
难度中等
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。
示例 1:
输入: 2 输出: [0,1,1]示例 2:
输入: 5 输出: [0,1,1,2,1,2]进阶:
- 给出时间复杂度为**O(n*sizeof(integer))的解答非常容易。但你可以在线性时间O(n)**内用一趟扫描做到吗?
- 要求算法的空间复杂度为O(n)。
- 你能进一步完善解法吗?要求在C++或任何其他语言中不使用任何内置函数(如 C++ 中的 __builtin_popcount)来执行此操作。
思路
动态规划,参考官方题解。
以 7 为例,它的二进制形式为 111,一共 3 个 1,也就是比 6 多了个末尾的 1。
由此可以联想到,对于奇数来说,它们的二进制 1 的个数都比它们的前一个数字多一个,即最后一个 0 => 1。
由此得到递推式1:res[i] = res[i-1] + 1
再次思考偶数的递推方式,对于 12 的二进制 1100,它的 1 的个数和 6 的二进制 110 相同,因为 12 是 6 的两倍,即左移一位。
因此,对于偶数来说,它们的二进制位数和它们除以二之后的数字相同。
由此得到递推式2:res[i] = res[i//2]
本题的 Base case 为 res[0] = 0,因为 0 的二进制还是 0,没有1。
代码
/**
* @param {number} num
* @return {number[]}
*/
var countBits = function(num) {
const res = new Array(num + 1).fill(0);
for(let i = 1; i <= num; i++) {
if (i % 2 == 1){
res[i] = res[i-1] + 1;
} else {
res[i] = res[i/2];
}
}
return res
};
class Solution:
def countBits(self, num: int) -> List[int]:
res = [0]*(num+1)
for i in range(1,num+1):
if i % 2 == 1:
res[i] = res[i-1] + 1
else:
res[i] = res[i//2]
return res
3.2
真就准备前缀和月呗。
题目
304. 二维区域和检索 - 矩阵不可变
难度中等
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2)。
上图子矩阵左上角 (row1, col1) = **(2, 1)** ,右下角(row2, col2) = **(4, 3),**该子矩形内元素的总和为 8。
示例:
给定 matrix = [ [3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5] ] sumRegion(2, 1, 4, 3) -> 8 sumRegion(1, 1, 2, 2) -> 11 sumRegion(1, 2, 2, 4) -> 12说明:
- 你可以假设矩阵不可变。
- 会多次调用 sumRegion 方法*。*
- 你可以假设 row1 ≤ row2 且 col1 ≤ col2。
思路
是昨天题目的二维版本,很明显有两种解法。
- 看作是多行的一维前缀和数组,构造函数时间复杂度为
O(mn), 查询区域和的时间复杂度为O(N) - 直接看作二维的前缀和数组,即每一个位置的数代表的是从左上角加到这个位置的总和。构造函数时间复杂度
O(mn),查询区域和的时间复杂度O(1)
我为了继续熟悉 JS 语法,就使用了简单的第一种方法。
代码
/**
* @param {number[][]} matrix
*/
var NumMatrix = function(matrix) {
const m = matrix.length;
if(m>0){
const n = matrix[0].length;
this.allSums = new Array(m).fill(0).map(() => new Array(n + 1).fill(0));
for(let i = 0;i<m;i++){
for (let j = 1;j<n+1;j++){
this.allSums[i][j] = this.allSums[i][j-1] + matrix[i][j-1];
}
}
}
};
/**
* @param {number} row1
* @param {number} col1
* @param {number} row2
* @param {number} col2
* @return {number}
*/
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
let res = 0;
for(let i = row1; i <= row2; i++){
res += this.allSums[i][col2+1]-this.allSums[i][col1];
}
return res;
};
/**
* Your NumMatrix object will be instantiated and called as such:
* var obj = new NumMatrix(matrix)
* var param_1 = obj.sumRegion(row1,col1,row2,col2)
*/
3.1
题目
303. 区域和检索 - 数组不可变
难度简单
给定一个整数数组
nums,求出数组从索引i到j(i ≤ j)范围内元素的总和,包含i、j两点。实现
NumArray类:
NumArray(int[] nums)使用数组nums初始化对象
int sumRange(int i, int j)返回数组nums从索引i到j(i ≤ j)范围内元素的总和,包含i、j两点(也就是sum(nums[i], nums[i + 1], ... , nums[j]))示例:
输入: ["NumArray", "sumRange", "sumRange", "sumRange"] [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]] 输出: [null, 1, -1, -3] 解释: NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]); numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3) numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))提示:
0 <= nums.length <= 104-105 <= nums[i] <= 1050 <= i <= j < nums.length- 最多调用
104次sumRange方法
思路
前缀和数组,利用一个数组来记录数组前n项的和。
代码
class NumArray:
def __init__(self, nums: List[int]):
sums = [0]
for i in nums:
sums.append(i+sums[-1])
self.sums = sums
def sumRange(self, i: int, j: int) -> int:
return self.sums[j+1]-self.sums[i]
# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(i,j)
/**
* @param {number[]} nums
*/
var NumArray = function(nums) {
const n = nums.length;
this.sums = new Array(nums.length+1).fill(0);
for(let i = 1;i<n+1;i++){
this.sums[i] = this.sums[i-1] + nums[i-1];
}
};
/**
* @param {number} i
* @param {number} j
* @return {number}
*/
NumArray.prototype.sumRange = function(i, j) {
return this.sums[j+1]-this.sums[i];
};
/**
* Your NumArray object will be instantiated and called as such:
* var obj = new NumArray(nums)
* var param_1 = obj.sumRange(i,j)
*/