Astar算法求解迷宫最短路 | Python实现

实验内容

给定一个二维数组模拟迷宫，0表示允许通过，1表示有障碍无法通过。

给定一个起点(x0, y0)和终点(x1, y1)，设计两种不同估价函数的A*算法，找到从起点走到终点的路径。

输入

Problem2.txt

  • 第一行给入口坐标x0, y0
  • 第二行给出口坐标x1, y1
  • 下面n行给一个n*m的0-1矩阵，表示迷宫

1,1

5,5

0 0 0 0 0

1 0 1 0 1

0 0 1 1 1

0 1 0 0 0

0 0 0 1 0

输出

Astar.txt

  • 共需要多少步
  • 路径坐标序列

共需13步

(1,1)-(1,2)-(2,2)-(3,2)-(3,1)-(4,1)-(5,1)-(5,2)-(5,3)-(4,3)-(4,4)-(4,5)-(5,5)

Astar算法

原理简介

A*算法是一种求解最短路径的直接搜索方法，是许多其他问题的常用启发式算法。

算法的核心公式$f(n) = g(n) + h(n)$

  • f(n)是从初始状态经由状态n到目标状态的代价估计，简写为F
  • g(n)是在状态空间中从初始状态到状态n的实际代价，简写为G
  • h(n)是从状态n到目标状态的最佳路径的估计代价，简写为H

通过计算这三个值，我们可以找到更具有更高尝试价值的路径。

会有两个数组来存储一些结点

  • open list：待检查的结点列表，路径可能经过，也可能不经过
  • close list：已经检查完毕的结点列表

搜索过程

  1. 把起点加入open list
  2. 循环
    • 遍历open list，查找F值最小的结点，把它作为当前要处理的结点
    • 把这个结点移到close list
    • 遍历当前这个结点四周的八个结点
      • 如果结点不可达或者它已经在close list中，就忽略
      • 如果它不在open list中，就加入open list中，并且把当前的结点设置成它的父节点，记录该结点的F, G, H值
      • 如果它已经在open list中，检查这条路径是否更好，以G值作为参考。G值越小表示路径越好。如果更好，就把它的父结点设置成当前的方格，并且重新计算G和F值。
    • 退出循环的情况
      • 终点已经在open list中，说明已经找到了路径
      • open list为空，表示已经没有路可以走了
  3. 保存路径

数据结构

为了方便记录每个点的父节点以及计算F, G, H值，需要自己定义一个结点类

class Node:

  1. 定义结点类的构造方法

    def __init__(self, x, y):
    self.pre = None
    self.x = x
    self.y = y
    self.update()

  2. 更新启发函数的值

    • 首先计算H的值，有两种方式

      1. 当前结点到目标结点的曼哈顿距离

        abs(node.x - target[0])+abs(node.y - target[1])

      2. 当前结点到目标结点的欧式距离

        (node.x - target[0])**2+(node.y - target[1])**2

    • 再计算G的值，即深度，这里指当前走的步数

    • 最后计算启发函数的值，F = G + H

    # 更新启发函数的值
def update(self):
    self.update_H()
    self.update_G()
    self.update_F()

# H值是和目标状态的距离之和
def update_H(self):
    # 用曼哈顿距离表示和目标的距离之和
    x, y = self.x, self.y
    self.H = abs(x - target[0]) + abs(y - target[1])

# G值表示深度，即当前走的步数
def update_G(self):
    if self.pre:
        self.G = self.pre.G + 1
    else:
        self.G = 0

# F是启发函数 F = G + H
def update_F(self):
    self.F = self.G + self.H

  3. 输出路径

    # 输出路径
def get_path(self):
    nodes = []
    node = self
    while node:
        nodes.append(node)
        node = node.pre
    res = []
    for i in nodes[::-1]:
        res.append("(" + str(i.x) + "," + str(i.y) + ")")
    return res

  4. 返回下一步可能所在的位置坐标

    • directions是我们自己定义的一个数组，用来快速向四个方向扩散

      directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]

    # 找到下一步可能所在的位置
def get_next_positions(self):
    next_positions = []
    for i, j in directions:
        next_x = i + self.x
        next_y = j + self.y
        if next_x >= 0 and next_x < len(maze) and next_y >= 0 and next_y < len(maze[0]):
            if maze[next_x][next_y] == 0:
                next_positions.append([next_x, next_y])
    return next_positions

I/O相关

  1. 从文件中读取文本

    def read_file(file_name):
    lines = []
    with open(file_name, encoding="utf-8") as f:
        lines = f.readlines()
    return lines

  2. 根据读取的文本生成迷宫

    def get_maze(lines):
    matrix = []
    for line in lines[2:]:
        line = line.strip()
        tmp = [int(i) for i in line.split(" ")]
        matrix.append(tmp)
    return matrix

  3. 写文件

    def write_file(file_name, lines):
    with open(file_name, 'w', encoding="utf-8") as f:
        for line in lines:
            f.write(str(line))

Astar搜索函数

根据算法描述转换成代码实现即可

def a_star(x0, y0):
    open_list, close_list = [], []
    # 初始化起点结点
    node = Node(x0, y0)
    open_list.append(node)
    while open_list:
        # 按照启发函数的值升序进行排列
        open_list.sort(key = lambda x: x.F)
        # 找到F值最小的结点，尝试扩展
        cur_node = open_list[0]
        # 确认是否是终点
        if cur_node.H == 0:
            print("wow, we find the path!")
            return cur_node.get_path()
        # 对当前这个F值最小的结点尝试搜索
        open_list.pop(0)
        close_list.append(cur_node)
        # 获取下一步可能的位置
        next_positions = cur_node.get_next_positions()
        for next_position in next_positions:
            x, y = next_position
            # 把下一个位置初始化为一个结点next_node
            next_node = Node(x, y)
            # 把cur_node设置成next_node结点的父节点
            next_node.pre = cur_node
            # 更新一下F G H值
            cur_node.update()
            # 判断next_node在close_list和open_list中的情况
            open_res = in_list(next_node, open_list)
            close_res = in_list(next_node, close_list)
            open_idx = open_res[1]
            # 如果在close_list中说明已经检查完毕，跳过即可
            if close_res[0]:
                continue
            # 如果在open_list中，需要判断是否更优
            if open_res[0] and next_node.F < (open_list[open_idx]).F:
                open_list[open_idx] = next_node
            # next_node不在open_list也不在close_list中
            if not open_res[0] and not close_res[0]:
                open_list.append(next_node)
  • main函数
if __name__ == "__main__":
    lines = read_file("Problem2.txt")
    maze = get_maze(lines)
    start, end = lines[0].rstrip(), lines[1].rstrip()
    start = start.split(",")
    end = end.split(",")
    x0, y0, x1, y1 = int(start[0])-1, int(start[1])-1, int(end[0])-1, int(end[1])-1
    target[0], target[1] = x1, y1
    path = a_star(x0, y0)
    lines = []
    lines.append("共需" + str(len(path)) + "步\n")
    lines.append("-".join(path))
    write_file("Astar.txt", lines)

运行结果

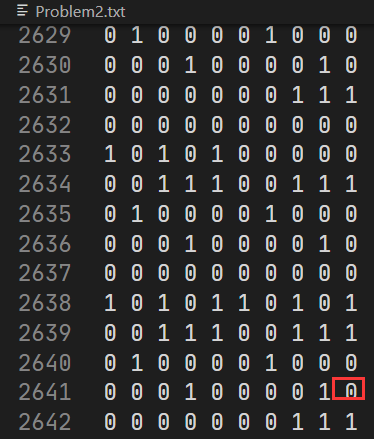
为了明显对比出两个启发函数的区别，我自己构造了一个2640*10的迷宫（没使用并查集，只是随便复制的）

  • 起点1，1
  • 终点2639，10，图中圈出来的那个

image-20201215214934390

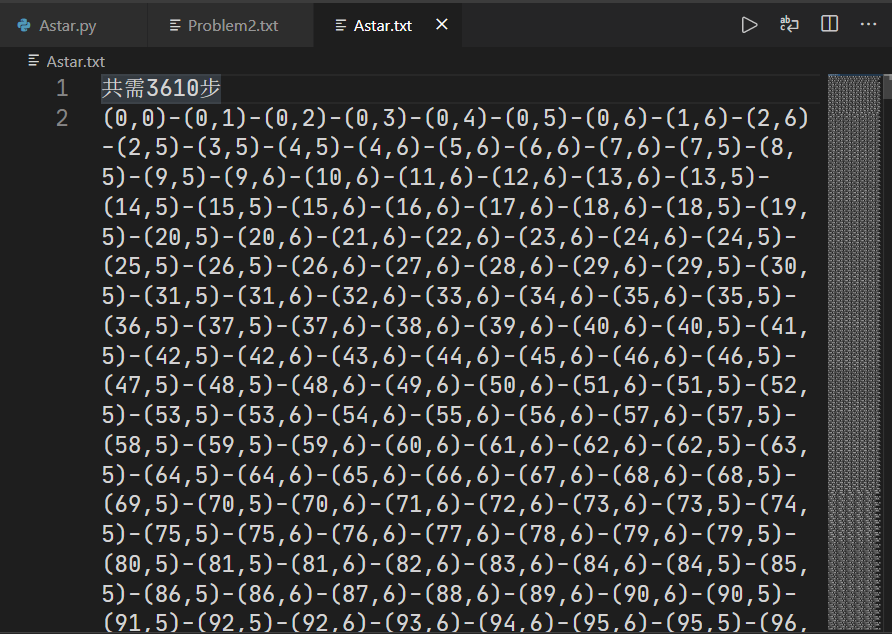
  1. 以曼哈顿距离作为启发函数

    image-20201215215802594

    image-20201215215656531

  2. 以欧式距离的平方作为启发函数

    image-20201215215846116

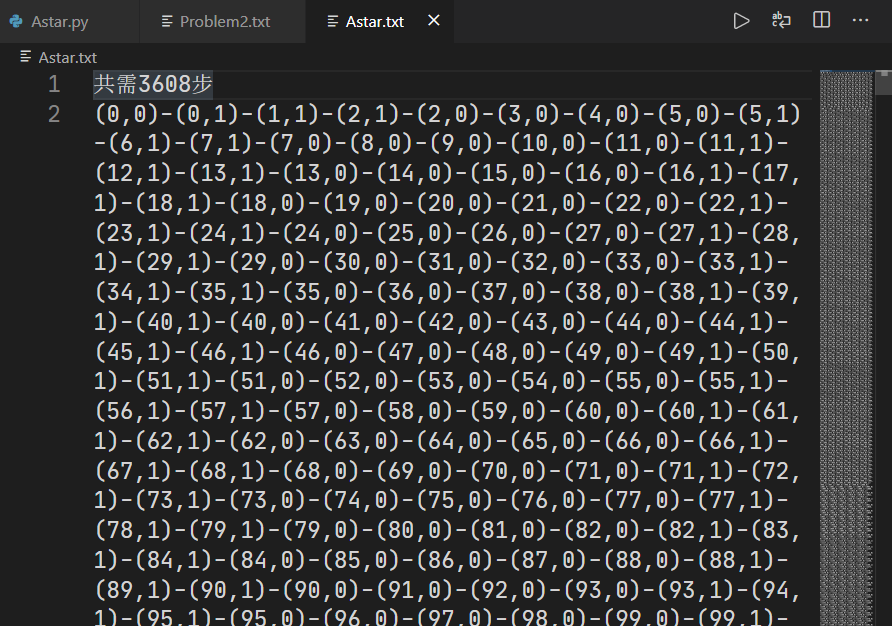
    image-20201215215901203

多次实验发现，在当前迷宫中，曼哈顿距离的启发函数花的时间远超欧氏距离的启发函数。

当然，这并不能直接的出哪个函数更优秀的结论，由于我本身只自定义了一个迷宫