八数码问题的深搜和广搜解法 | Python实现

八数码问题简介

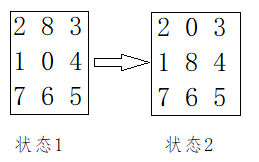
在3×3的棋盘上，摆有八个棋子，每个棋子上标有1至8的某一数字。棋盘中留有一个空格，空格用0来表示。空格周围的棋子可以移到空格中。

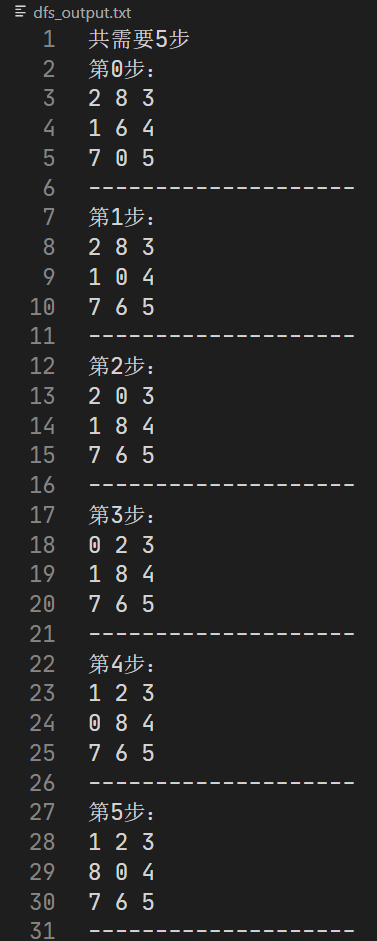
要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为123804765），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

img

数据结构

为了记录每个每一步走的状态，我们需要自己定义一个棋盘类Board（类似结点）。

我们主要用到的属性有两个：前驱棋盘self.pre和步数self.steps。

class Board:

  1. 首先需要定义棋盘的构造方法

    • 初始化它的前驱为空
    • 初始化它的棋盘矩阵
    • 同时更新它的步数（在一开始实例化的时候步数为0，因为前驱结点为空）
    # 初始化棋盘状态，matrix为棋盘的矩阵
def __init__(self, matrix):
    self.pre = None
    self.matrix = matrix
    self.update_steps()
# 根据父结点的步数来计算当前结点走的步数
def update_steps(self):
    if self.pre:
        self.steps = self.pre.steps + 1
        else:
            self.steps = 0

  2. 定义打印棋盘结点的方式

    • 一行行打印即可
    # 打印棋盘
def show(self):
    res = []
    res.append("第" + str(self.steps)+"步：\n")
    for i in range(3):
        res.append(" ".join([str(j) for j in self.matrix[i]]) + "\n")
    res.append("-" * 20+"\n")
    return res

  3. 从当前整个路径的根节点开始打印

    • 不断找前驱结点，把每个棋盘的打印放入列表中
    # 打印从根节点开始到当前节点的路径
def show_path(self):
    path = []
    node = self
    while node:
        path = node.show()+path
        node = node.pre
    path = ["共需要"+str(self.steps)+"步\n"] + path
    return path

  4. 定位0的方法

    • 返回0所在横坐标和纵坐标
    # 找到0当前在棋盘中的位置
def find_zero(self):
    for i in range(3):
        for j in range(3):
            if self.matrix[i][j] == 0:
                return i, j

  5. 获取下一步可能的所有棋盘矩阵

    • 先找到0的位置
    • 然后尝试把0和上下左右的棋子交换位置，如果合法，就把可能的矩阵添加到数组中
    • 最后返回一个三维的数组
    # directions数组用来记录0可能的走的四个方向
directions = [[0, 1], [1, 0], [0, -1], [-1, 0]]
# 下一步可能的棋盘
def next_possible_boards(self):
    res = []
    i, j = self.find_zero()
    for direction in self.directions:
        x, y = direction
        if i + x >= 0 and i + x <= 2 and j + y >= 0 and j + y <= 2:
            next_board = copy.deepcopy(self.matrix)
            next_board[i][j], next_board[i + x][j +y] = next_board[i + x][j + y], next_board[i][j]
            res.append(next_board)
    return res

  6. 将棋盘序列化，即把棋盘的矩阵转成字符串

    • 这是为了在遍历的时候更加方便地实现去重
    # 将当前棋盘序列化，二维数组=>字符串
def serialize(self):
    tmp = ""
    for i in self.matrix:
        tmp += "".join([str(j) for j in i])
        return tmp

  7. 判断是否到达目标状态

    • 直接将当前棋盘序列化后和123804765对比

文件I/O

  1. 读取文件

    def read_file(file_name):
    lines = []
    with open(file_name, encoding="utf-8") as f:
        lines = f.readlines()
    return lines

  2. 将从文件中读取的内容转换成矩阵

    def get_matrix(lines):
    matrix = []
    for line in lines:
        line = line.strip()
        tmp = [int(i) for i in line.split(" ")]
        matrix.append(tmp)
    return matrix

  3. 写文件

    def write_file(file_name, lines):
    with open(file_name, 'w', encoding="utf-8") as f:
        for line in lines:
            f.write(str(line))

BFS

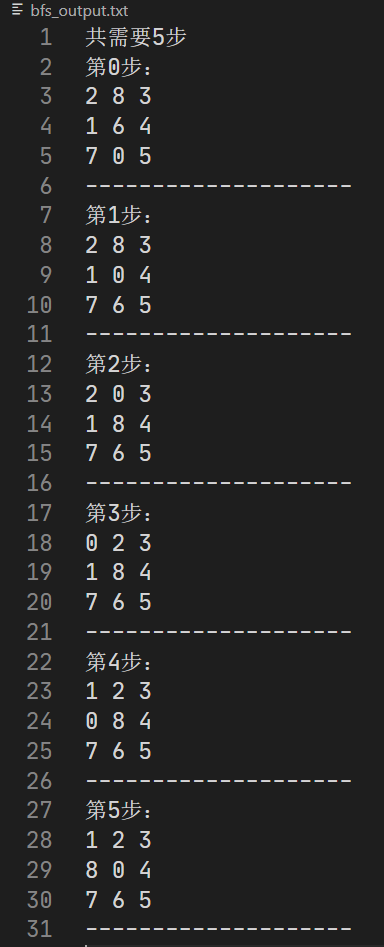
  • 整体流程

undefined

BFS_8puzzle.py

  • 算法实现
    • 用一个数组去模拟队列，每一次遍历一层
    • 遍历的时候，获取每个可能的棋盘的下一步棋盘，添加到下一次遍历的队列里
    • 为了避免重复遍历，我们定义了一个visited集合，里面存储了已经遍历过的可能性的棋盘序列
def bfs(b):
    # visited数组用来取消一些
    visited = set()
    queue = []
    queue.append(b)
    level = 0
    while queue:
        show_cur_level(queue, level)
        # 每次遍历一层
        tmp = []
        for board in queue:
            if board.finished():
                path = board.show_path()
                write_file("bfs_output.txt", path)
                return
            next_boards = board.next_possible_boards()
            for matrix in next_boards:
                next_board = Board(matrix)
                if next_board.serialize() not in visited:
                    visited.add(next_board.serialize())
                    next_board.pre = board
                    next_board.update_steps()
                    tmp.append(next_board)
        queue = tmp
        level += 1
image-20201212151853950

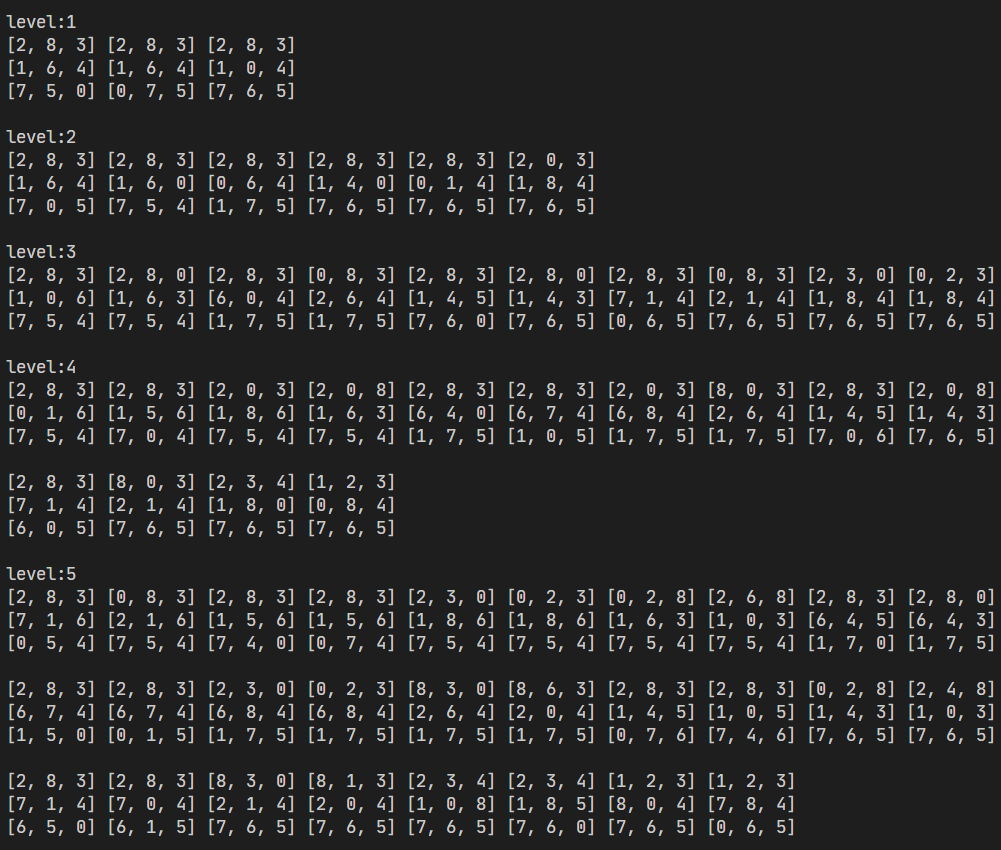
我也定义了一个函数，较清晰地展示每一层的情况

def show_cur_level(queue, level):
    # 打印某个层级的所有棋盘
    print("level:" + str(level))
    for i in range(0, len(queue), 10):
        for j in range(i, min(i+10, len(queue))):
            print(queue[j].matrix[0], end=" ")
        print()
        for j in range(i, min(i+10, len(queue))):
            print(queue[j].matrix[1], end=" ")
        print()
        for j in range(i, min(i+10, len(queue))):
            print(queue[j].matrix[2], end=" ")
        print("\n")
image-20201212152829761

DFS

  • 整体流程

undefined

  • 算法实现
    • 用一个递归函数来实现每次向下遍历
    • 设定最大递归深度为10
    • 同样的，利用visited集合来避免一条路上走回头路
    • 向下遍历完之后运用回溯法的思想，消除回头路的证据
image-20201212151728247